Scanner (1)

1. Introduction

Scanner作为front-end的第一阶段, 也称为lexical analyzer, 负责读取字符流并获取单词, 若单词合法, 则为其分配词类(part of speech), 否则报错. 以下是scanner用到的一些模型:

1. recogizer: 用于识别字符流中的单词
2. regular expression: 一种用于定义syntax(语法)的符号形式
3. 一系列将regular expression转换为recognizer的构造法
4. 多种scannr实现方法: table-driven scanner, direct-coded scanner, hand-coded scanner

为实现为每个单词分配词类, scanner会使用一种描述programming language的词汇结构, 称为microsyntax(微语法). Microsyntax负责将字符拼成单词, 或将单词拆分为字符. 大多数编程语言将blank(空格)或punctuation(标点)作为单词分隔符, 由一个或多个alphanumeric character(字母字符, 包括a-z, A-Z, 0-9)组成的单词称为identifier(标识符), 但规定首字符必须不能为数字.
大多数编程语言还定义了另一种单词, 称为keyword(关键字)或reserved word(保留字). Keyword具有特殊意义, 例如C和Java中的while和static, 并拥有自己的词类. 所以当程序中包含while单词时, 即便while符合identifier的定义, scanner只将其识别为keyword.

2. Recognize Words

识别单词最简单的方法就是逐个字符查看. 假设需要检测keyword new, 现有NextChar()函数可逐个输出代码中的字符, 以下为实现代码:

c ← NextChar();
if (c = 'n')
  c ← NextChar();
  if (c = 'e')
    c ← NextChar();
      if (c = 'w')
        report success;
      else 
        try something else;
  else 
    try something else;
else 
  try something else;

上述代码可总结为以下transition diagram(转换图):

上图中, start state(初始状态)记为$s_0$, accepting state(接收状态)记为$s_3$, 用双层圆圈表示. 只有输入的单词为new时才会抵达$s_3$. 可用相同方式构建一个识别keyword while的recognizer, 其transition diagram如下:

为识别多个单词, 可从同一state发出多个边. 下图的transition diagram表示可识别单词new和not的recognizer: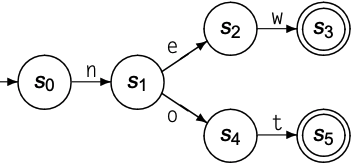

将上述所有recognizer结合后, 即可识别new, not和while: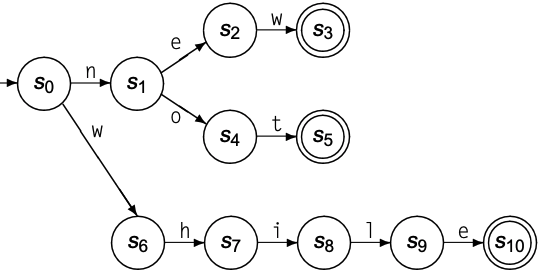

2.1 A Formalism for Recognizer

Transition diagram可以作为代码的抽象表示, 也可看做形式化的数学模型, 称为finite automata(FA, 有限自动机). 形式上, finite automata为一个五元组$(S, \sum, \delta, s_0, S_A)$:

• $S$: 有限状态集, 也就是transition diagram中所有圆圈, 包括$s_e$(error state)
• $\sum$: 有限字母集, 也就是transition diagram中所有边的标签
• $\delta(s, c)$: 转换函数, 表示state之间转换的公式, 其中$s \in S, c \in \sum$. 当state $s_i$遇到输入字符$c$时, FA将采取$s_i \xrightarrow{c} \delta(s, c)$
• $s_0$: start state(初始状态)
• $S_A$: 所有accept state集合, 也就是transition diagram中所有双层圆圈, $S_A \in S$

以上一节识别new, not和while为例, 可写作以下FA形式:
\begin{equation}
S = {s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9, s_{10}, s_e} \\
\sum = {e, h, i, l, n, o, t, w} \\
\delta = \begin{cases}
s_0 \xrightarrow{n} s_1, \quad s_0 \xrightarrow{w} s_6, \quad s_1 \xrightarrow{e} s_2, \quad s_1 \xrightarrow{o} s_4, \quad s_2 \xrightarrow{w} s_3 \\[2ex]
s_4 \xrightarrow{t} s_5, \quad s_6 \xrightarrow{h} s_7, \quad s_7 \xrightarrow{i} s_8, \quad s_8 \xrightarrow{l} s_9, \quad s_9 \xrightarrow{e} s_{10}
\end{cases} \\
s_0 = s_0 \\
S_A = {s_3, s_5, s_{10}}
\end{equation}

对于其他的状态转换, 可定义为$\delta(s_i, c) = s_e$, 其中$s_e$表示error state. FA只能接收以$s_0$开始的字符串, 当字符串处理完毕后, 最后所处的state应为accepting state或error state. 以new为例, 从$s_0$开始, 完成于$s_3$, 因此FA会接收该字符串; 对于nut, 从$s_0$开始, $s_0 \xrightarrow{n} s_1$, $s_1 \xrightarrow{u} s_e$, FA一旦进入$s_e$, 则会直接返回$s_e$.
当字符串$\textit{x}$ 包含字符$x_1, x_2, x_3 \ldots x_n$, 有且只有满足以下公式时, 字符串$\textit{x}$ 会被$FA(S, \sum, \delta, s_0, S_A)$接收:
$$
\delta(\delta(\ldots\delta(\delta(\delta(s_0, x_1), x_2), x_3)\ldots, x_{n-1}), x_n) \in S_A
$$

上述公式表示, 从$s_0$开始, 对字符串$\textit{x}$ 中每个字符$x_i$调用$\delta$进行状态切换, 若最终状态为accepting state, 则FA接收该字符串. 但也存在另外两种情况:

1. FA在处理字符时遇到错误, 并切换到$s_e$
2. FA对每个字符都进行状态切换, 但最后状态不为accepting state

上述两种情况皆被FA识别为error, 并会通知用户.

2.2 Recognize More Complex Words

上述recoginzer可以识别明确规定的字符串或字符串集合, 例如not. 但如果用于识别数字这类模糊的定义, 则显得很困难. 以下是识别数字的transition diagram: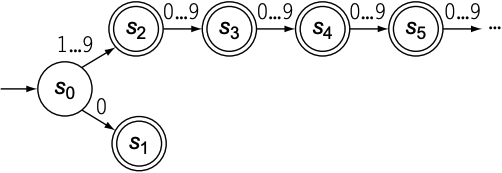

除了$s_0 \xrightarrow{0} s_1$为了处理特殊情况0外, $s_1, s_2, s_3, \ldots$的状态转移条件都是相同的. 由于该FA从$s_2$后的状态切换没有终点, 所以违反了有限的原则; 且由于从$s_2$开始, 路径上所有状态都是等价的(皆为accpeting state且状态转移条件相同).
之所以FA识别数字很困难, 因为数字属于一个词类(part of speech), 而13属于词素(lexeme)
通过允许Fstate添加环(cycle)可简化FA, 以下是识别数字的transition diagram: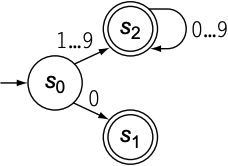

当实现上述transition diagram时, 不能只用$\textit{if-else}$语法, 还需要$\textit{while}$来实现循环. 可以用表来定义$\delta$:

$\delta$	0	1	2	3	4	5	6	7	8	9	Other
$s_0$	$s_1$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_e$
$s_1$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$
$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_2$	$s_e$
$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$	$s_e$

通过表可得到FA的五元组:
\begin{equation}
S = {s_0, s_1, s_2, s_e} \\
\sum = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} \\
\delta = \begin{cases}
s_0 \xrightarrow{0} s_1, \quad s_0 \xrightarrow{\text{1-9}} s_2 \\[2ex]
s_2 \xrightarrow{\text{0-9}} s_2, \quad s_1 \xrightarrow{\text{0-9}} s_e
\end{cases} \\
s_0 = s_0 \\
S_A = {s_1, s_2}
\end{equation}

FA可以作为recoginzer的规则, 但这种方式并不简洁.

3. Regular Expression

被FA接收的所有单词结合称为ℱ, 由这些单词组成的语言称为$\textit{L}(ℱ)$. FA的transition diagram虽然能描述该语言, 但不够直观, 因此需要regular expression(RE, 正则表达式)来描述语言, 通过RE描述的语言称为regular language. RE的规定如下:

• 若只识别单个单词, 如new, 则RE为new
• 若需识别两个单词, 如new和while, 则RE为new|while
• 若识别的单词有重复前缀, 如new和not, 则RE为n(ew|ot), |表示或. 其FA的transition diagram如下:
  

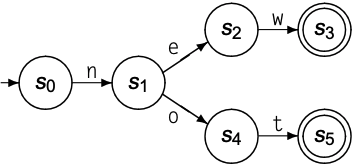
最后剩下一种情况, 循环. RE使用$x^{*}$的方式表示x的零或多次出现, *操作符被称为Kleene closure, 或简称closure(闭包). 以下是用RE表示的数字词类:
$$
0|(1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)^{*}
$$

3.1 Formalize the Notation

RE中字母表$\sum$中字符串的集合, 外加一个空字符串$\epsilon$, 形成了RE的language. 对于指定RE r, 其语言为$\textit{L}(r)$. 假设R和S各为字符串, RE的三种基本操作如下:

• Alternation(选择): 表示两个字符串的并集, 记作$R|S$, 定义为$\{x|x \in R \ or \ x \in S\}$
• Concatenation(连接): 表示两个字符串的连接, 记作$RS$, 定义为$\{x|x \in R \ and \ x \in S\}$
• Closure(闭包): 表示R的闭包, 记作$R^{*}$, 定义为$\bigcup_{i=0}^{\infty}{R^i}$, 也可以当做零次或多次R的自身连接

Closure还包括finite closure(有限闭包), 记作$R^i$, 表示字符串R出现$[1, i]$次. 例如: $R^3$等价于$(R|RR|RRR)$. 还有一种closure成为positive closure(正闭包), 表示R至少出现1次, 等价于$RR^{*}$.

通过以上三种操作, 字母表$\sum$会拥有以下特性:

1. 若$a \in \sum$, 则$a$也是一个RE
2. 若$r$和$s$为RE, 分别表示$\textit{L}(r)$和$\textit{L}(s)$, 那么$r|s$也是RE, 表示$\textit{L}(r)$和$\textit{L}(s)$的并集; $rs$也为RE, 表示$\textit{L}(r)$和$\textit{L}(s)$的连接; $r^{*}$也是RE, 表示$\textit{L}(r)$的kleene closure.
3. $\epsilon$也是一个RE, 表示仅包含空串的集合

RE中的操作符优先级从高到低: 括号, 闭包, 连接, 选择. 为方便表示一个字符范围, 可只给出第一个和最后一个元素, 中间用省略号代替, 例如: $[0 \cdots 9]$表示十进制数字集合, 等同于$(0|1|2|3|4|5|6|7|8|9)$

3.2 Examples

以下是使用RE表示microsyntax的例子:

1. Algol中identifier: 首字符必须为alphabetic character, 其余字符可为number或alphabetic character. RE表示为$([A \cdots Z]|[a \cdots z])([A \cdots Z]|[a \cdots z]|[0 \cdots 9])^{*}$
2. 无符号整数: RE表示为$0|[1 \cdots 9][0 \cdots 9]^{*}$
3. 无符号实数: RE表示为$(0|[1 \cdots 9][0 \cdots 9]^{*} (\epsilon |.[0 \cdots 9]^{*}))$, 前半部分负责检测整数位, 后半段负责检测小数位
4. 求补运算符: 使用^可简化RE, 例如Java中的字符串可表示为$"(\textrm{^"})^{*}"$
5. Java中使用**//**作为注释的开端, 直到行末尾都为注释内容, 可表示为$//(\textrm{ˆ\n})^{*}\textrm{\n}$. 若是多行注释符, 以/*开始, 以*/结束, 则RE为$\textrm{/*}(\textrm{^*|*+^/})^{*}\textrm{*/}$

以第五个例子Java的多行注释为例, 由RE构建的FA如下图: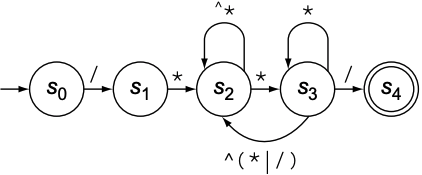

可以看到, RE和FA之间的关系不再name明显, 原因在于从$s_2$到$s_3$的状态转换: 当recognizer识别到*字符时, 无论下一个字符是否为/, 都需要正确的处理. 以汇编语言中的寄存器命名为例: 字母r开头, 后接一个整数, 对应的RE应为$r[0 \cdots 9]^+$; 但实际中寄存器数量是有限的, 假设只能有32个寄存器, 则RE应为$r([0 \cdots 2]([0 \cdots 9]|\epsilon)|[4 \cdots 9]|(3(0|1|\epsilon)))$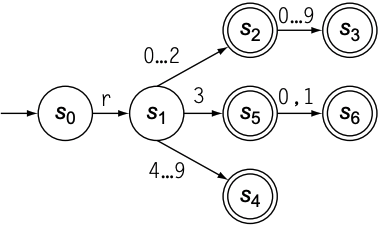

虽然FA变得更复杂, 但对于同等长度的字符串来说, FA的处理时间是相通的. FA的开销只与输入字符串的长度有关, 因为每个单字符只进行一次状态转移. 如果觉得上述RE不易理解, 可使用一个更简单的RE:
$$
r0|r00|r1|r01|r2|r02|r3|r03|r4|r04|r5|r05|r6|r06|r7|r07|r8|r08|r9|r09|r10| \\
r11|r12|r13|r14|r15|r16|r17|r18|r19|r20|r21|r22|r23|r24|r25|r26|r27|r28|r29|r30|r31
$$

3.3 Closure Properties of REs

当一个或一组RE经过操作后, 仍是RE, 这就是RE的闭包性质. 连接操作允许我们从简单的RE构建复杂的RE, Kleene closure让我们用简洁的方式构建无限集, 选择操作允许我们对多个语法范畴取并集, 有限闭包使得我们可定义庞大且有限的集合.

4. From RE to Scanner

RE虽然能形式化表示语言, 但不能直接被运行, 还需要构造成FA. 以下是RE构建FA所需的算法:

• Thompson’s construction: 从RE到NFA
• Subset construction: 从NFA到DFA
• Hopcroft’s algorithm: 最小化DFA

整个从RE到DFA的过程图如下: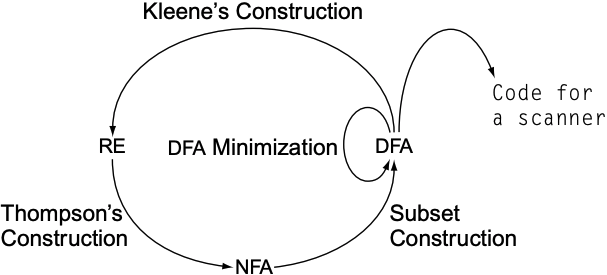

在阐述几种构造FA前, 需要区分FA(或称DFA, Deterministic finite automata)和NFA(Non-deterministic finite automata)的差别.

4.1 Non-deterministic Finite Auotmata

RE的字符集中包含$\epsilon$, 但之前所有FA中都没有$\epsilon$作为状态转移的条件. 一般$\epsilon$用于连接多个复杂的FA. 例如以下图中的$\text{FA}_m$和$\text{FA}_n$: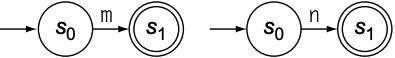

为了将两个FA结合为 $\text{FA}_{mn}$, 需用 $\epsilon$ 连接$\text{FA}_{m}$的accpet state和$\text{FA}_n$的start state, 结果如下:

从$s_2$到$s_3$称为$\epsilon$-$transition$, 这种状态不会改变输入字符串的读写位置, 因为不会消耗任何输入字符. 虽然逻辑上没有任何影响, 但会造成冗余, 可通过合并$s_2$和$s_3$来消除$\epsilon$-$transition$, 结果如下图: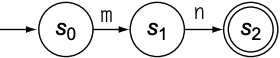

但有时$\epsilon$-$transition$会复杂化FA的合并, 以$a^{*}$和$ab$为例, 其FA如下: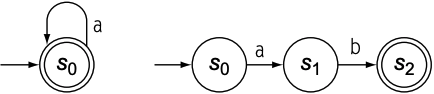

当使用$\epsilon$-$transition$合并两个FA后, 可得到$a^{*}ab$, 其FA如下: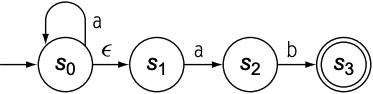

当FA处于$s_0$状态, 输入字符为$a$时, 存在两个转移路径:

1. $s_0 \xrightarrow{a} s_0$
2. $s_0 \xrightarrow{\epsilon} s_1, s_1 \xrightarrow{a} s_2$

若输入字符串为aab, 则$s_0$应走路线1; 若输入字符串为ab, 则$s_0$应走路线2. $s_0$是否正确转移状态不再取决于当前输入的字符, 而是要考虑后面的字符, 这违背了顺序读取字符的规则, 所以若FA中某个状态$s_i$对单个字符存在多条转移路径时, 则称为非确定性有限自动机(NFA). 若FA中每个状态对于单个字符都有唯一的转移路径, 则称为确定性有限自动机(DFA).

针对NFA的行为, 存在两种模型:

1. 每次NFA进行非确定性选择时, 若存在使输入字符串转向accpeting state的转移存在, 则采用该转移路径.
2. 每次NFA进行非确定性选择时, NFA都克隆自身以追踪每种转移的结果. NFA更像是一个状态的集合, 每个状态代表一个克隆体来处理某个非确定性选择. 当NFA耗尽输入字符串, 且处于accepting state时, NFA会接收该字符串.

上述模型中, $NFA(S, \sum, \delta, s_0, S_A)$接受一个输入字符串$x_1, x_2, x_3 \cdots x_k$的充分必要条件为: 至少存在一条状态转移路径, 始于$s_0$, 终于某个状态$s_k \in S_A$. NFA和DFA在表达力上是等价的, 任何DFA都是某个NFA的特例, 因此任何NFA都可以通过一个DFA模拟.
若NFA采用第二种模型, 对于每个非确定性选择都复制本身, 每个复制得到的NFA都称为一个configuration. 对于一个拥有$n$个状态的NFA, 最多会产生$|\sum|^n$. 以上述RE为例, $a^{*}ab$的DFA为: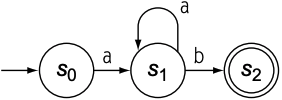

上述FA的RE其实应写作$aa^{*}b$, 但由于$aa^{*}b$和$a^{*}ab$定义的单词集是相同的, 所以该DFA与NFA也是等价的.

4.2 RE to NFA: Thompson's Construction

以下是Thompson's construction对于单个输入字符所有RE操作的FA构建: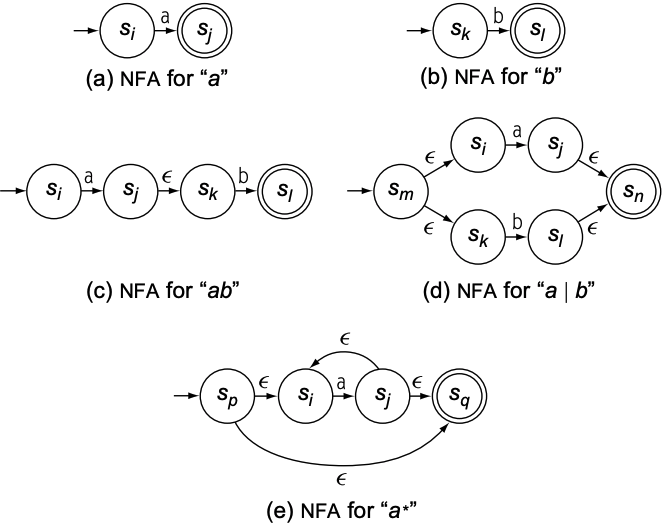

假设RE为$a(b|c)^{*}$, 为了构建NFA, 需要按照以下步骤:

1. 为$a$, $b$, $c$构建NFA
   

2. 为$b|c$构建NFA
   

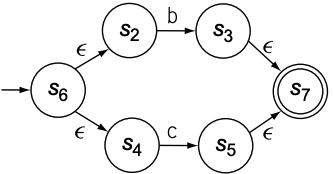
3. 然后创建$(b|c)^{*}$
   

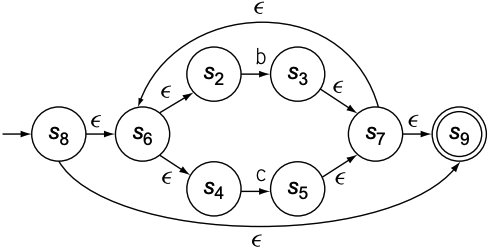
4. 最后将$a$和$(b|c)^{*}$连接
   

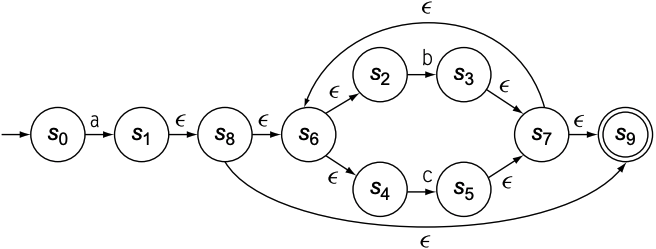
Thompson's construction构建的NFA具有以下几个特性:

• 每个NFA都只有一个start state和一个accepting state
• 使用$\epsilon$-$transition$来连接多个NFA
• 每个状态至多有2个转入或转出的$\epsilon$-$transition$
• 每个状态至多有1个转入或转出的字符转移

4.3 NFA to DFA: The Subset Construction

上一节提供了从RE到NFA的方法, 这一节负责将NFA转换为DFA, 让状态转换变得确定. Subset construction以$\text{NFA}(N, \sum, {\delta}_N, n_0, N_A)$为输入, 生成一个$\text{DFA}(D, \sum, {\delta}_D, d_0, D_A)$, 其中, NFA和DFA拥有相同的字符表$\sum$, 但其他部分不一定相同. 以下为subset construction算法:

$q_0$ $\leftarrow$ $\epsilon$-closure({$n_0$});
Q $\leftarrow$ $q_0$;
WorkList $\leftarrow$ {$q_0$};

while (WorkList $\neq$ $\emptyset$) do
  remove q from WorkList;
  for each character c $\in$ $\sum$ do
    t $\leftarrow$ $\epsilon$-closure(Delta(q, c));
    T[q, c] $\leftarrow$ t;
    if t $\notin$ Q then
      add t to Q and to WorkList;
  end;
end;

其中, $\epsilon$-$closure(s_i)$表示从某状态$s_i$出发, 仅通过$\epsilon$-$transition$所能到达的所有状态, 这些状态是等价的. $Delta(q, c)$表示从configuration q中读取字符c时能到达的所有configuration. 整个算法的过程描述如下:

1. 从$n_0$出发, 通过$\epsilon$-$transition$能达到的所有状态(包含$n_0$), 这些状态构成了$q_0$
2. 将Q置为$q_0$, 并将$q_0$做一个configuration放入名为$\text{WorkList}$的configuration set中
3. 若$\text{WorkList}$不为空, 则保持循环
4. 从$\text{WorkList}$中取出一个configuration, 称为$q$
5. 对于字符表$\sum$中的每个字符$c$, 进行如下操作:
6. 找到$q$输入字符$c$后所能转移到的新configuration, 称为$t$
7. 将该次转移记录在表$T$中
8. 若$t$没有出现在$Q$中, 则将t加入到$Q$和$\text{WorkList}$

$Q$是单调递增的. 由于NFA中的configuration数量是有限的, 每个configuration只会出现一次, 所以while循环总会停止运行. 在循环停止时, $Q$包含了NFA中所有有效的configuration, $T$包含所有configuration间的转移. $Q$最大有$|2^N|$个configuration, NFA中非决定性选择数量决定了configuration set的大小. 当subset construction运行后就已经构造了一个DFA模型, 每个configuration $q_i \in Q$都需要一个状态$d_i \in D$来表示. 若$q_i$中包含NFA中的accepting state, 则$d_i$为DFA的accepting state; $q_0$对应的$d_0$即为start state. 遵循$q_i$到$d_i$的映射, 可从T构造出转移函数${\delta}_D$.

以$a(b|c)^{*}$为例, 其NFA如下: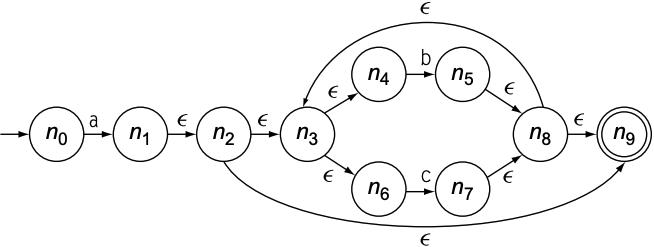

算法步骤如下:

1. $q_0$设置为$\epsilon$-$closure(n_0)$, 也就是$n_0$. $Q$和$\text{WorkList}$也为$n_0$
2. 每次while迭代时, 需从$\text{WorkList}$中取出一个configuration, 名为$q$, 并对$\sum$中所有字符(a, b, c)分别进行$\epsilon$-$closure(Delta(q, x))$计算(x表示字符a, b或c)
3. 第1次while迭代: 取出$q_0$(也就是$n_0$)并计算:

• a返回$q_1$: $n_1, n_2, n_3, n_4, n_6, n_9$, 添加到$\text{WorkList}$中
• b和c返回: 空集

4. 第2次while迭代: 取出$q_1$并计算:

• a返回: 空集
• b返回$q_2$: $n_5, n_8, n_9, n_3, n_4, n_6$, 添加到$\text{WorkList}$中
• c返回$q_3$: $n_7, n_8, n_9, n_3, n_4, n_6$, 添加到$\text{WorkList}$中

5. 第3次while迭代, 取出$q_2$并计算:

• a返回: 空集
• b返回: $q_2$, 不添加重复configuration到$\text{WorkList}$中
• c返回: $q_3$, 不添加重复configuration到$\text{WorkList}$中

6. 第4次while迭代: 取出$q_3$并计算:

• a返回: 空集
• b返回: $q_2$, 不添加重复configuration到$\text{WorkList}$中
• c返回: $q_3$, 不添加重复configuration到$\text{WorkList}$中

7. $\text{WorkList}$为空, 退出while循环

以下是subset construction各次迭代过程表:

nth Loop	Set Name	DFA States	NFA States	a	b	c
1	$q_0$	$d_0$	$n_0$	\begin{Bmatrix} n_1, n_2, n_3 \\ n_4, n_6, n_9 \end{Bmatrix}	none	none
2	$q_1$	$d_1$	\begin{Bmatrix} n_1, n_2, n_3 \\ n_4, n_6, n_9 \end{Bmatrix}	none	\begin{Bmatrix} n_5, n_8, n_9 \\ n_3, n_4, n_6 \end{Bmatrix}	\begin{Bmatrix} n_7, n_8, n_9 \\ n_3, n_4, n_6 \end{Bmatrix}
3	$q_2$	$d_2$	\begin{Bmatrix} n_5, n_8, n_9 \\ n_3, n_4, n_6 \end{Bmatrix}	none	$q_2$	$q_3$
4	$q_3$	$d_3$	\begin{Bmatrix} n_7, n_8, n_9 \\ n_3, n_4, n_6 \end{Bmatrix}	none	$q_2$	$q_3$

通过上述4个DFA的状态可得以下FA图: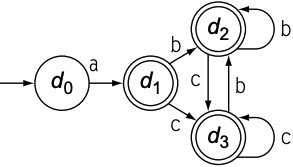

以下是一种离线计算$\epsilon$-closure()的方法:

for each state $n \in N$ do
  $E_n \leftarrow {n}$
end;
WorkList $\leftarrow$ N
while (WorkList $\neq$ $\emptyset$) do
  remove n from WorkList
  t $\leftarrow$ {n} $\cup$ ${\bigcup}_{n \xrightarrow{\epsilon} p \in {\delta}_N}$
  if t $\neq$ $E_n$
    $E_n$ $\leftarrow$ t
    WorkList $\leftarrow$ WorkList $\cup$ {m|m$\xrightarrow{\epsilon}$n $\in$ ${\delta}_N$}
  end;
end;

算法步骤如下:

1. 初始化: 为NFA的每个状态节点$n$创建一个集合$E_n$, 表示从$n$出发的所有$\epsilon$-$transition$; 集合$\text{WorkList}$表示NFA中所有状态节点
2. 若集合$\text{WorkList}$不为空, 则保持循环:
3. 从集合$\text{WorkList}$取出一个状态节点$n$
4. 计算从$n$出发的所有$\epsilon$-$transition$, 命名为$p$, 并通过$p$获得$E_p$, 将所有$E_p$和$n$的并集命名为集合$t$
5. 若$t$不等于$E_n$, 说明需要更新$E_n$:
   1. $E_n$替换为t
   2. 将$n$的所有前趋$\epsilon$-$transition$节点$m$加入到WorkList中, 保证前趋节点也可以更新集合$E_m$

4.4 DFA to Minimal DFA: Hopcroft’s Algorithm

作为RE到DFA的最后一步, 负责减少DFA中的状态数目. Subset construction产生的冗余状态节点虽然不会影响扫描字符串的时间, 但会增加recognizer所占内存空间, 更小的recognizer更适合载入到cache中.
为最小化$\text{DFA}(D, \sum, \delta, d_0, D_A)$中的状态数量, 需要判断两个状态是否等价, 即两者对任何输入字符是否产生同样的行为. 以下是Hopcroft’s Algorithm代码:

Split(S) {
  for each c $\in$ $\sum$ do
    if c splits S into $s_1$ and $s_2$
      return {$s_1$, $s_2$};
  end;
  return S;
}

T $\leftarrow$ {$D_A$, {$D − D_A$}};
P $\leftarrow$ $\emptyset$
while (P $\neq$ T) do
  P $\leftarrow$ T;
  T $\leftarrow$ $\emptyset$;
  for each set p $\in$ P do
    T $\leftarrow$ T $\cup$ Split(p);
  end;
end;

算法步骤:

1. 将所有状态划分为两类: $p_0 = D_A$和$p_1 = {D - D_A}$, 分别表示接收状态和非接收状态
2. 若状态集合$P$与$T$不等, 则保持循环:
3. $P$代表上次集合划分的结果, $T$表示这次集合划分的结果
4. 对同一集合的所有状态进行等价性划分

对于状态划分的解释: 若存在两个状态$d_i$, $d_j$对于所有输入字符都有相同的行为, 则它们同属于一个DFA状态集合. 例如: $d_i \xrightarrow{c} d_x, d_j \xrightarrow{c} d_y$, 而$d_i, d_j \in p_s$, 那么$d_x, d_j$也必定属于同一集合. 该算法不会跟踪集合中每个状态对于所有输入字符的行为, 而是针对单个输入字符的行为进行划分, 例如: 对于字符$c \in \sum$, $c$对于每个状态$d_i \in p_s$都必须产生同样的行为, 否则拆分$p_s$.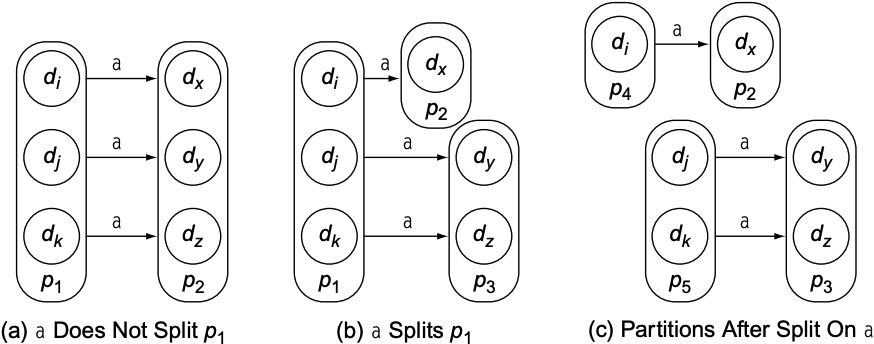

以$fee|fie$为例, 其DFA如下图: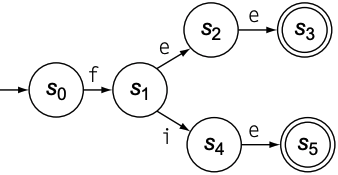

以下是最小化DFA的算法步骤:

1. 将所有状态分为接收状态集合($\{s_3, s_5\}$)和非接收状态集合($\{s_0, s_1, s_2, s_4\}$)
2. 由于$\{s_3, s_5\}$没有任何向外的转移, 所以无法拆分
3. 集合$\{s_0, s_1, s_2, s_4\}$对字符$e$进行状态转移, 由于$\{s_2, s_4\}$行为相同, 因此将其拆分出来
4. 集合$\{s_0, s_1\}$对字符$f$进行状态转移, 将$s_0$拆分出来
5. 最后剩下四个集合: $\{s_3, s_5\}, \{s_0\}, \{s_1\}, \{s_2, s_4\}$

最小化DFA后的transition diagram为:

对于上一节提到的$a(b|c)^{*}$的DFA, 通过Hopcroft’s Algorithm最小化DFA后, 只留下两个状态集合: $\{\{d_0\}, \{d_1, d_2, d_3\}\}$, 所以最后transition diagram应如下图: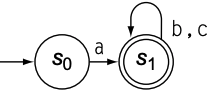

4.5 Use a DFA as a Recognizer

现在我们已经可以根据一个RE构建出对应的DFA, 假设一个programming language有多个语法范畴, 对应的RE: $r_1, r_2, r_3, \cdots, r_k$, 则可为所有语法范畴构造一个单一的RE, 即$(r_1|r_2|r_3|\cdots|r_k)$.
对于RE可进行上述整个过程: 构建NFA, 根据NFA构建DFA, 最小化DFA并转换为可执行代码. 当编译器接收到输入字符串时, 该代码可对输入字符串的每个字符进行考察, 并在最后判定是否处于accepting state. 如果是, 则接收该字符串; 如果不是, 则存在两种情况: 可能读取位置已经超过了一个或多个accepting state, 需要回溯; 也可能未经过任何accepting state, 该字符串无效.
实际上, 我们需要对RE指定优先级, 这样匹配到多个模式时返回最高优先级的语法范畴. 也需要为无法构成有效单词的文本指定RE, 例如: space, tab, end-of-line. 这样recognizer才会递归地返回结果.