1. Implement Scanners

三种将DFA转换为可执行代码的方法:

  • table-driven scanner
  • direct-coded scanner
  • hand-coded scanner

上述所有scanner都会模拟DFA的方式: 重复读取输入字符串中的每个字符, DFA状态转移, 并最终停止与某个状态. 若停止于accepting state, 则返回该单词的词素及其语法范畴; 若不是accepting state, 则需要判断状态转移路径上有没有遇到过accepting state并回溯到合适的状态节点.

1.1 Table-Driven Scanner

Table-driven scanner需要使用一个skeleton scanner和一个table, compiler用户负责提供lexical pattern, 一般由RE表示. Scanner generator负责用于驱动skeleton scanner的table. 假设RE为$r[0\cdots9]^{+}$, 则生成的table如下:
The Classifier Table, CharCat

The Classifier Table, CharCat

The Transition Table, δ

The Transition Table, δ

The Token Type Table, Type

The Token Type Table, Type

skeleton scanner代码如下:

NextWord()
  state $\leftarrow$ $s_0$;
  lexeme $\leftarrow$ "";
  clear stack;
  push(bad);

  while (state $\neq$ $s_e$) do
    NextChar(char);
    lexeme $\leftarrow$ lexeme + char;
    if state $\in$ $S_A$
      clear stack;
    push(state);
    cat $\leftarrow$ CharCat[char];
    state $\leftarrow$ $\delta$[state,cat];
  end;

  while (state $\notin$ $S_A$ and state $\neq$ bad) do
    state $\leftarrow$ pop();
    truncate lexeme;
    RollBack();
  end;

  if state $\in$ $S_A$
    return Type[state];
  else
    return invalid;

上述代码中, 若第一个while循环结束时不属于accepting state, 则进入第二个while循环来回溯到最近的accpeting state. 对于某些RE可能会导致大量回滚, 影响scanner的运行时间. 假设RE为$ab|(ab^{*}c)$为例, 以下是其DFA: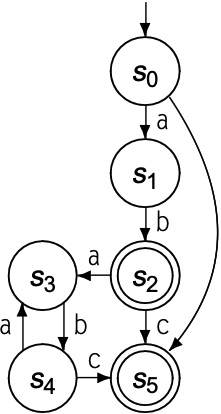
The DFA of ab(ab)<sup>*</sup>c

假设输入字符串为ababababc, scanner将读取所有字符, 并返回认为该字符串符合RE规定; 但若输入字符串为abababab, scanner运行步骤如下:

  1. 扫描所有字符, while循环的终止状态不为accepting state, 回滚至最近的accepting state, 也就是ab, 剩下ababab
  2. 扫描所有字符, 循环后回滚, 返回ab, 剩下abab
  3. 扫描所有字符, 循环后回滚, 返回ab, 剩下ab
  4. 扫描所有字符, 无需回滚, 返回ab

为避免多次回滚问题, 需要一个全局计数器InputPos来记录输入流中的位置, 二维比特数组Failed来记录scanner扫描时发现的死胡同, 横坐标为state, 纵坐标为输入字符串的读取位置InputPos.

InitializeScanner()
  InputPos = 0;
  for each state s in the DFA do
    for i = 0 to |input stream| do
      Failed[s, i] ← false;
    end;
  end;

NextWord()
  state $\leftarrow$ $s_0$ ;
  lexeme $\leftarrow$ "";
  clear stack;
  push($\langle$bad, bad$\rangle$);

  while (state $\neq$ $s_e$) do
    NextChar(char);
    InputPos $\leftarrow$ InputPos + 1;
    lexeme $\leftarrow$ lexeme + char;
    if Failed[state, InputPos]
      break;
    if state $\in$ $S_A$
      clear stack;
    push($\langle$state, InputPos$\rangle$);
    cat $\leftarrow$ CharCat[char];
    state $\leftarrow$ $\delta$[state,cat];
  end;

  while(state $\notin$ $S_A$ and state $\neq$ bad ) do
    Failed[state, InputPos] ← true;
    $\langle$state, InputPos$\rangle$ ← pop();
    truncate lexeme;
    RollBack();
  end;

  if state $\in$ $S_A$
    return TokenType[state];
  else 
    return bad;

假设RE和输入字符串不变, scanner运行步骤如下:

  1. 将Failed数组中所有元素置为false, 并将InputPos置为0
  2. 扫描所有字符, while循环的终止状态不为accepting state, 回滚至最近的accepting state, 也就是ab, 剩下ababab. 回滚期间会将stack中所有失败路径的$\langle \text{state}, \text{InputPos} \rangle$在Failed中设置为true, 包括$\langle s_2, 3 \rangle, \langle s_3, 4 \rangle, \langle s_4, 5 \rangle, \cdots$
  3. 第二次扫描字符时, 会在读取完前两个字符ab后中断, 因为$\text{Failed}[s_2, 3] == true$. 返回ab, 剩下abab.
  4. 第三次扫描字符同上, 会在读取完前两个字符ab后中断. 返回ab, 剩下ab
  5. 扫描并返回ab

可以看到, 这一优化通过空间换时间的方式, 记录那些不可能导向accepting state的路径, 因此之后的字符串扫描会避开回滚.
给定一个DFA, scanner generator可为DFA中的每个字符创建一个列, 每一行表示一个状态. 遍历DFA时, 为每个转移字符设置对应生成的状态, 并将相同的多列合并为一列. 若DFA已经最小化, 则不存在合并问题.

1.2 Direct-Coded Scanner

为提高table-driven scanner的性能, 可以将$\text{cat} \leftarrow \text{CharCat}[char]$和$\text{state} \leftarrow \delta[state,cat]$这两步合并, 节省DFA状态转移时间.
虽然这两次查找的时间都在$O(1)$量级, 但当我们从CharCat表中取出第i个元素时, 需要计算该元素地址: $@\text{CharCat} + i \times w$, 其中$@\text{CharCat}$表示CharCat表的起始地址, w表示每个元素所占字节数; 而$\delta$的元素取操作更复杂: $@\delta + (\text{state} \times \text{number_of_columns} + \text{cat}) \times w$, 其中$@\delta$表示$\delta$的起始地址, w表示每个元素所占字节数. 每次while循环都需要要进行两次地址计算操作, 并从内存中加载.
因此, 在Direct-coded scanner中摒弃了CharCat表和$\delta$表, 而是为每个状态编写一段代码, 用代码片段的跳转替代查表操作. 若RE为$r[0 \cdots 9]^{+}$, 以下是Direct-coded scanner的代码:

$s_{init}$: 
  lexeme $\leftarrow$ "";
  clear stack;
  push(bad);
  goto $s_0$;

$s_0$:
  NextChar(char);
  lexeme $\leftarrow$ lexeme + char;
  if state $\in$ $S_A$
    clear stack;
  push(state);
  if (char = 'r')
    goto $s_1$;
  else
    goto $s_{out}$;

$s_1$:
  NextChar(char);
  lexeme $\leftarrow$ lexeme + char;
  if state $\in$ $S_A$
    clear stack;
  push(state);
  if ('0' $\leqslant$ char $\leqslant$ '9')
    goto $s_2$;
  else
    goto $s_{out}$;

$s_2$: 
  NextChar(char);
  lexeme $\leftarrow$ lexeme + char;
  if state $\in$ $S_A$
    clear stack;
  push(state);
  if ('0' $\leqslant$ char $\leqslant$ '9')
    goto $s_2$;
  else
    goto $s_{out}$

$s_{out}$:
  while (state $\notin$ $S_A$ and state $\neq$ bad) do
    state $\leftarrow$ pop();
    truncate lexeme;
    RollBack();
  end;
  if state $\in$ $S_A$
    return Type[state];
  else
    return invalid;

上述代码使得状态跳转无需查表, 通过goto语句可跳转至其他状态. 虽然提升了运行效率, 但也会破坏结构化程序设计的宗旨, 从而造成bug频出且代码可读性下降. 因此该代码应由scanner generator生成, 而不是由人工编写. 本例中对于字符的判断十分简单, 因为只需要对字符$r$, $[0-9]$和EOF进行判断; 但若字符分布比较分散, 则table-driven scanner效率更高.

1.3 Hand-Coded Scanner

虽然table-driven scanner和direct-coded scanner已经能保证单个字符的处理时间保持在常数量级, 大部分商业compiler仍然使用hand-coded scanner, 以此来减少scanner与compiler中其他组件的接口开销, 并且通过细节上的优化, 可以实现输入端读取字符效率的提高, 也可以提升输出端生成词素的效率.

1.3.1 Buffer the Input Stream

每次输入一个字符都需要进行I/O读取操作, 这显然开销过大, 因此可使用buffered I/O. 每次I/O操作不再读取单个字符, 而是读取一个固定长度的字符串, 并保存在buffer中. NextChar()函数直接从内存中读取, 不需要进行I/O操作, 这样每个字符的读取开销就平摊到一次字符串读取. 使用buffer和指针也有利于Rollback()操作, 只要没有越过buffer的起始位置, 都可以通过移动指针来实现回滚.
buffer for scanner

以下是NextChar()和Rollback()在双缓存下的实现代码:

Initialization()
  Input ← 0;
  Fence ← 0;
  fill Buffer[0 : n];

NextWord()
  Char $\leftarrow$ Buffer[Input];
  Input $\leftarrow$ (Input + 1) mod 2n;
  if (Input mod n = 0)
    fill Buffer[Input : Input+n-1];
    Fence $\leftarrow$ (Input + n) mod 2n;
  return Char;

Rollback()
  if (Input = Fence)
    signal roll back error;
  Input ← (Input - 1) mod 2n;

每读取一个字符, scanner会将指针地址**+1**, 然后2n取模; 每次回滚, 需要将指针地址**-1**, 然后2n取模. Input表示buffer的当前读取位置, Fence表示表示有效缓冲区的起始地址, 用于防止Rollback()操作超出范围.

1.3.2 Generate Lexemes

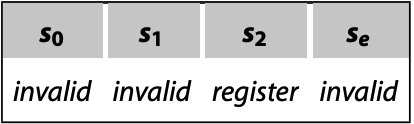
Table-driven scanner和direct-coded scanner都将输入字符累加到字符串lexeme中. 但scanner之后的parser有时无需获得原字符串, 而需要另一种形式的信息. 以register编号为例, compiler更在意register的整数编号, 而不是以r开头的字符串. 这时就需要在手动修改代码:

begin;
  RegNum $\leftarrow$ RegNum $\times$ 10 + (char - '0');
  goto $s_2$;
end;

有些scanner会识别注释和空白并丢弃, 这些scanner的优化会让整个编译效率提升.

1.4 Handle Keywords

一般来说, 我们会将所有keywords(关键字)放入RE, 生成DFA, 并通过scanner识别keyword. 但存在另一种方案: 将所有keyword都识别为identifier, 然后用hash table(散列表)判断该字符串是否为keyword. 因为对于hand-coded scanner来说, keyword数量的增加会让DFA中的状态数量明显增加, 为了平衡实现负担, 可使用perfect hashing(完美散列), 使用合适的hash function来生成一个无碰撞的整数集, 保证keyword查找所需的时间复杂度为$O(1)$.
若使用scanner generator创建recognizer, 则状态数量的增加不会导致编译效率下降(但会导致占用内存增加), 更适合将keyword的识别功能交给DFA.

2. Advanced Topics

2.1 DFA to Regular Expression

Thompson’s construction和subset construction已经证明DFA和RE有同等的表达力. 通过Kleene's construction可将一个DFA转换为同等的RE. 可将DFA的transition diagram看做一个有向图, $L(\text{DFA})$表示DFA中所有可接受的字符串集合, RE则需要表示$L(\text{DFA})$中所有字符串. 若DFA中有环, 则$L(\text{DFA})$中存在无限个的字符串, RE可用Kleene closure来表示所有环导致的子路径集合.
假设给定$\text{DFA}(D, \sum, {\delta}_D, d_0, D_A)$, 其中状态集为$\{d_0, d1, \cdots, d_n\}$, 算法代码如下:

for i = 0 to $|D|$ − 1
  for j = 0 to $|D|$ − 1
    $R_{ij}^{-1}$ = {$a \ | \ \delta(d_i, a) = d_j$}
    if (i = j) then
      $R_{ij}^{-1}$ = $R_{ij}^{-1} | \{\epsilon\}$
for k = 0 to $|D|$ − 1
  for i = 0 to $|D|$ − 1
    for j = 0 to $|D|$ − 1
      $R_{ij}^k$ = $R_{ij}^k(R_{ij}^{k-1})^{*}R_{ij}^{k-1} | R_{ij}^{k-1}$
$L$ = $R_{0j}^{|D|-1}, \ s_j \in D_A$

$R^{k}_{ij}$表示从状态节点$d_i$到状态节点$d_j$, 且不经过状态节点编号大于$k$的所有字符串集合, 每个$R^{k}_{ij}$都由一个RE表示, 以下是$R^{k}_{ij}$的几种特殊形式:

  1. $R^{-1}_{ij}$: 表示在不跨越任何节点的情况下, 从状态节点$d_i$到$d_j$. 表示状态节点$d_i$与$d_j$直连, $R^{-1}_{ij}$表示$\sum$中任意字符, 但不包括$\epsilon$.
  2. $R^{-1}_{ii}$: 表示在不跨越任何节点的情况下, 从状态节点$d_i$到其自身. 表示$d_i$的自身闭环, $R^{-1}_{ii}$表示$\sum$中任意字符, 且包括$\epsilon$
  3. $R^{n}_{0j}$: 由于$n$为状态节点的最大编号, 所以对跨越的节点不做任何限制的情况下, 从起始状态$d_0$到$d_j$的所有字符串集合, 其中$d_j \in D_A$, 等同于从start state到accepting state的所有可能的字符串, 也就是RE所能表示的所有字符串

为获得$R^{n}_{0j}$, 需要一个从$R^{-1}_{0j}$到$R^{n}_{0j}$的推导公式: $R^{k}_{ij} = R^{k-1}_{ik} (R^{k-1}_{kk})^{*} R^{k-1}_{kj} | R^{k-1}_{ij}$. 从$k-1$递进到$k$, 需将三条子路径首尾相连: 从i到k的子路径, 从k到自身的子路径, 从k到j的子路径, 且这三条子路径的状态编号不大于$k-1$. 也就是说, 将所有经过k的路径添加到$R^{k-1}_{ij}$中, 即可获得$R^{k}_{ij}$. RE的运算需要Kleene algebra, 以下面的DFA为例: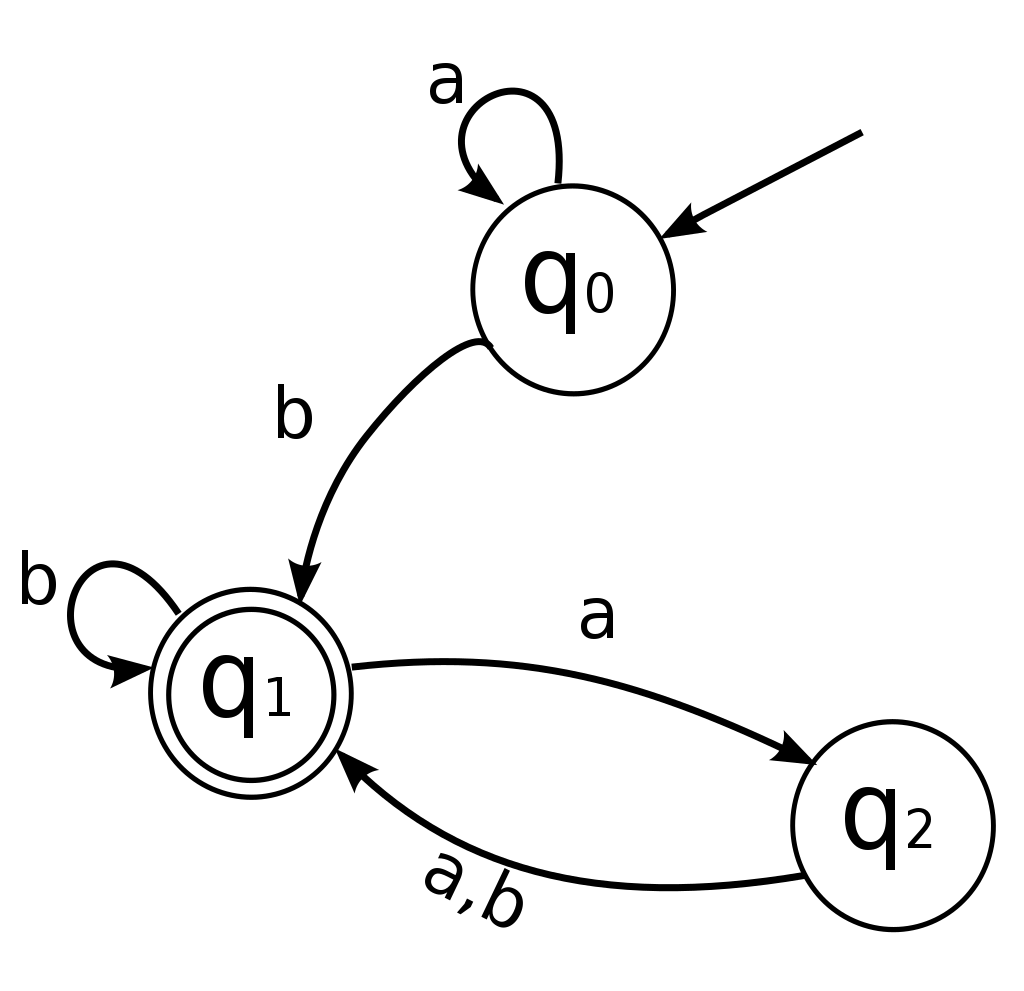
DFA Transition Diagram

首先初始化所有$R^{-1}_{ij}$:

$R^{-1}_{00} = a \ | \ \epsilon$
$R^{-1}_{01} = b$
$R^{-1}_{02} = \phi$
$R^{-1}_{10} = \phi$
$R^{-1}_{11} = b \ | \ \epsilon$
$R^{-1}_{12} = a$
$R^{-1}_{20} = \phi$
$R^{-1}_{21} = a \ | \ b$
$R^{-1}_{22} = \epsilon$

第一次循环, k = 0 (跨越状态编号为0的节点):

$R^{0}_{00} = R^{-1}_{00} (R^{-1}_{00})^{*} R^{-1}_{00} | R^{-1}_{00} = a^*$
$R^{0}_{01} = R^{-1}_{00} (R^{-1}_{00})^{*} R^{-1}_{01} | R^{-1}_{01} = a^*b$
$R^{0}_{02} = R^{-1}_{00} (R^{-1}_{00})^{*} R^{-1}_{02} | R^{-1}_{02} = \phi$
$R^{0}_{10} = R^{-1}_{10} (R^{-1}_{00})^{*} R^{-1}_{00} | R^{-1}_{10} = \phi$
$R^{0}_{11} = R^{-1}_{10} (R^{-1}_{00})^{*} R^{-1}_{01} | R^{-1}_{11} = b | \epsilon$
$R^{0}_{12} = R^{-1}_{10} (R^{-1}_{00})^{*} R^{-1}_{02} | R^{-1}_{12} = a$
$R^{0}_{20} = R^{-1}_{20} (R^{-1}_{00})^{*} R^{-1}_{00} | R^{-1}_{20} = \phi$
$R^{0}_{21} = R^{-1}_{20} (R^{-1}_{00})^{*} R^{-1}_{01} | R^{-1}_{21} = a \ | \ b$
$R^{0}_{22} = R^{-1}_{20} (R^{-1}_{00})^{*} R^{-1}_{02} | R^{-1}_{22} = \epsilon$

第二次循环, k = 1 (跨越状态编号为1的节点):

$R^{1}_{00} = R^{0}_{01} (R^{0}_{11})^{*} R^{0}_{00} | R^{0}_{00} = a^*$
$R^{1}_{01} = R^{0}_{01} (R^{0}_{11})^{*} R^{0}_{01} | R^{0}_{01} = a^*b^*b$
$R^{1}_{02} = R^{0}_{01} (R^{0}_{11})^{*} R^{0}_{02} | R^{0}_{02} = \phi$
$R^{1}_{10} = R^{0}_{11} (R^{0}_{11})^{*} R^{0}_{00} | R^{0}_{10} = \phi$
$R^{1}_{11} = R^{0}_{11} (R^{0}_{11})^{*} R^{0}_{01} | R^{0}_{11} = b*$
$R^{1}_{12} = R^{0}_{11} (R^{0}_{11})^{*} R^{0}_{02} | R^{0}_{12} = b^*a$
$R^{1}_{20} = R^{0}_{21} (R^{0}_{11})^{*} R^{0}_{00} | R^{0}_{20} = \phi$
$R^{1}_{21} = R^{0}_{21} (R^{0}_{11})^{*} R^{0}_{01} | R^{0}_{21} = (a|b)b^*$
$R^{1}_{22} = R^{0}_{21} (R^{0}_{11})^{*} R^{0}_{02} | R^{0}_{22} = (a|b)b*a|\epsilon$

第三次循环, k = 2 (跨越状态编号为2的节点):

$R^{2}_{00} = R^{1}_{02} (R^{1}_{22})^{*} R^{1}_{20} | R^{1}_{00} = a^*$
$R^{2}_{01} = R^{1}_{02} (R^{1}_{22})^{*} R^{1}_{21} | R^{1}_{01} = a^*b(a(a|b)b^*)^*$
$R^{2}_{02} = R^{1}_{02} (R^{1}_{22})^{*} R^{1}_{22} | R^{1}_{02} = a^*b^*b(a(a|b)b^*)^*a$
$R^{2}_{10} = R^{1}_{12} (R^{1}_{22})^{*} R^{1}_{20} | R^{1}_{10} = \phi$
$R^{2}_{11} = R^{1}_{12} (R^{1}_{22})^{*} R^{1}_{21} | R^{1}_{11} = (a(a|b)|b)^*$
$R^{2}_{12} = R^{1}_{12} (R^{1}_{22})^{*} R^{1}_{22} | R^{1}_{12} = (a(a|b)|b)^*a$
$R^{2}_{20} = R^{1}_{22} (R^{1}_{22})^{*} R^{1}_{20} | R^{1}_{20} = \phi$
$R^{2}_{21} = R^{1}_{22} (R^{1}_{22})^{*} R^{1}_{21} | R^{1}_{21} = (a|b)(a|(a|b)|b)^*$
$R^{2}_{22} = R^{1}_{22} (R^{1}_{22})^{*} R^{1}_{22} | R^{1}_{22} = ((a|b)b^*a)^*$

该DFA中start state为$q_0$, accepting state为$q_1$, 因此RE为$R^2_{01}$, 也就是$a^{*}b(a(a|b)|b)^{*}$

2.2 Another Approach to DFA Minimization: Brzozowski’s Algorithm

之前提到使用subset construction将NFA转化为DFA, 原理在于消除重复前缀路径, 这给了Brzozowski一个将NFA直接变为minimal DFA的思路: 假设存在一个NFA $n$, Brzozowski’s Algorithm的算法过程如下:

  1. reverse(n): 反转$n$中所有转移的方向, 将原本的start state改为accepting state, 并添加一个新的start state, 连接至原本的accepting state
  2. subset(n): 利用subset construction合并所有相同前缀路径的状态
  3. reachable(n): 丢弃所有无关状态和转移
  4. 再次重复上述三部

Brzozowski’s Algorithm的算法也可总结为:
$$reachable(subset(reverse(reachable(subset(reverse(n))))))$$

内层的reachable, subset和reverse负责消除NFA中重复的后缀路径; 外层的reachable, subset和reverse负责消除NFA中重复的前缀路径. 以$abc|bc|ad$为例, 其NFA图如下: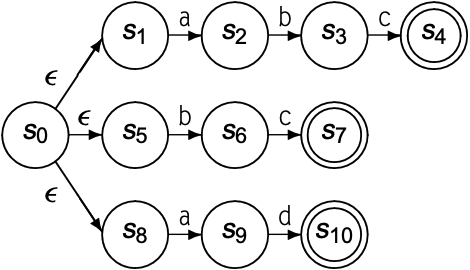
NFA for abc|bc|ad

反转NFA的所有转移方向, 并添加一个新的start state, 名为$s_{11}$: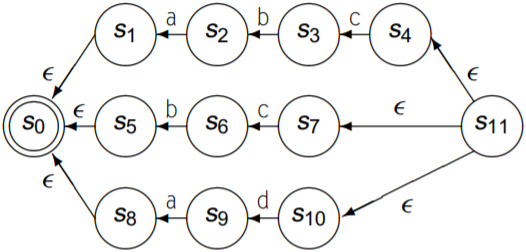
Reverse the NFA

使用subset(n)消除NFA中重复的后缀路径: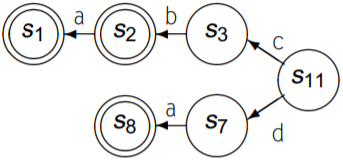
Subset the NFA

再次反转NFA的所有转移方向: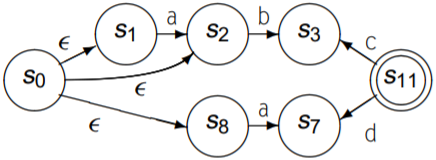
Reverse the DFA

再进行subset(n)消除NFA中重复的前缀路径: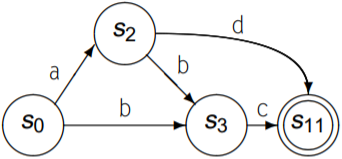
Subset the NFA to Produce the Minimal DFA

虽然看似要进行两次subset导致复杂度提升, 但其实执行起来很快, 也比较容易实现.

2.3 Closure-Free Regular Expression

RE中的子类在词法分析之外也有应用, 该子类就是closure-free regular expression, 例如: $w_1 | w_2 | w_3 | \cdots | w_n$, 其中$w_i$都是$\sum$中字符连接构成. 这种RE有一个性质, 其transition diagram是无环的.
很多字符串的识别问题都可以用这种无闭包RE描述, 例如词典的单词, 过滤的URL或散列表中的键. 为构建无闭包RE的DFA, 需从$s_0$状态开始, 沿新单词对应的转移路径前进, 直到耗尽输入或到达$s_e$. 若输入耗尽, 则将新单词对应的最终状态指定为accepting state; 若到达$s_e$, 则向DFA添加一条路径. Recognizer识别每个输入字符只需要常数时间.
使用这种方法构造出的DFA不能保证是最小的, 例如: deed, feed, seed的无环DFA如下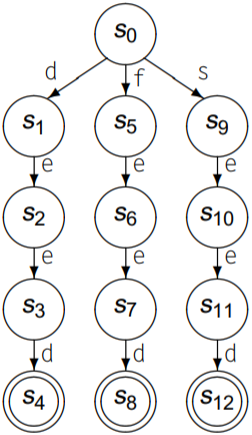
Subset the NFA to Produce the Minimal DFA

三条路径都有共同后缀eed, 所以最小化可以合并$(s_2, s_6, s_{10})$, $(s_3, s_7, s_{11})$, $(s_4, s_8, s_{12})$