1. Introduction

Pattern matching(模式匹配)又称字符串匹配问题, 问题可描述为: 给定字符串S和T, 判断S是否包含T(通常$|S| \gg |T|$), 其中T被称为pattern(模式串).

2. Brute Force

该算法的思路很简单: 比较S的第一个字符和T的第一个字符, 若相等, 则继续比较两个字符串的第二个字符; 否则T回退到第一个字符, 并和S的第二个字符比较, 以此类推, 直到S或T的所有字符比较完毕.

int search(String s, String t) {
    for (int i = 0; i < s.length(); i++) {
        int j = 0;
        while (j < t.length() && s.charAt(i+j) == t.charAt(j)) {
            j++;
        }
        if (j == t.length()) return i;
    }
    return -1;
}

假设S和T中的字符平均分布, 因此S[0] = T[0]的概率为$\frac{1}{26}$, S[1] == T[1]的概率为$\frac{1}{26^2}$, 假设S的长度为M, 则预期复杂度为$O(M)$; 但S和T中的字符并不是平均分布的, 假设S的长度为M, T的长度为N, 则最差时间复杂度为$O(MN)$.

3. Knuth-Morris-Pratt

3.1 Brute Force

假设S为"AAAAAAAAAB", T为"AAAAB", Brute Force匹配字符串时会出现多次重复, 如下图:

  0 1 2 3 4 5 6 7 8 9
  A A A A A A A A A B
1 A A A A B
2   A A A A B
3     A A A A B
4       A A A A B
5         A A A A B
6           A A A A B

上图中, 第一次匹配失败后, brute force会将T向右移动一位并尝试匹配, 直到第六次匹配成功: 由于T的最后一位字符为B, 而S[0:4]均为A, 因此第二次到第五次匹配并没有必要, 可直接跳过S[0:4], 直接从S[5]开始匹配.

3.2 Skip Impossible Iteration

可以发现, brute force完全忽略了第一次匹配得到的信息: S的子字符串与S的前缀子字符串相同, 且两个子字符串的长度相同. 若想降低brute force的复杂度, 则需减少比较字符的次数, 而KMP的核心思想在于跳过不可能匹配成功的字符. 假设S为"ABCABC", T为"ABCABD", brute force的步骤如下:

   0 1 2 3 4 5 6 7
   A B C A B C
1  A B C A B D
2    A B C A B D
3      A B C A B D
4        A B C A B D

第一次匹配时, 匹配停在了第六位字符(S[5] != T[5]), 说明S[0:5] == T[0:5], 即ABCAB. 第一次匹配时我们可知"AB"出现在S[0:1]和S[3:4], 且"AB"为T的前缀字符串, 因此让T向右移动一位或两位没有意义, 只有让T向右移动三位才能匹配到S的下一个"AB".
假设S[i] != T[j], 则上述过程可看作: S依然停留在i坐标, T向右移动以跳过不可能匹配成功的位置, 并重新比较S[i]. 因此, S不会回退, 也不会反复比较S中已匹配成功过的字符; 匹配失败时, 已匹配成功的子字符串长度为j, 因此T的移动范围为[1,j], 1表示向右移动一位, j表示T[0:j-1]之间不存在任何需要尝试匹配的位置; 由于S[i-j:i-1] == T[0:j-1], 因此T已经拥有所有信息, 向右移动多少位无需考虑S的字符.

3.3 Prefix Function

给定一个长度为n的字符串a, 则prefix function(前缀函数)为一个长度为n的数组$\pi$, 其中$\pi[i]$的定义为:

  • 若$a[0:i]$有一对相等的前缀和后缀: a[0:k-1]和a[i-(k-1):i], 那么$\pi[i]$就是这个前缀(或后缀)的长度, 即$\pi[i] = k$
  • 若存在多对相等的前后缀, 则$\pi[i]$为最长一对的长度
  • 若不存在相等的前后缀, 则$\pi[i] = 0$

总结来说, $\pi[i]$是a[0:i]的最长相等前后缀的长度. 假设a为"ABCABCD":

  • $\pi[0] = 0$: 规定$\pi[0]$为0
  • $\pi[1] = 0$: AB不存在相等前后缀
  • $\pi[2] = 0$: ABC不存在相等前后缀
  • $\pi[3] = 1$: ABCA存在一对相等前后缀(a[0]与a[3])
  • $\pi[4] = 2$: ABCAB存在一对相等前后缀(a[0:1]与a[3:4])
  • $\pi[5] = 3$: ABCABC存在一对相等前后缀(a[0:2]与a[3:5])
  • $\pi[6] = 0$: ABCABCD不存在相等前后缀

因此, s的前缀函数为[0,0,0,1,2,3,0]. 之所以介绍前缀函数, 因为T的移动取决于前后缀: 假设a为S和T的公共子字符串, 则T的移动一定满足相等的前后缀. 以上一节的S和T为例, S为"ABCABC", T为"ABCABD", 第一次匹配停在第六位字符, 即公共子字符串a为"ABCAB", T在向右移动后仍需匹配公共字符串a的后缀, 因此T的前缀需等于a的后缀, 而T的前缀也是a的前缀, 也就需计算a的相等前后缀.
现在的问题在于如何高效地计算前缀函数, 最容易想到的方法是逐个字符对比:

int[] prefix(String a) {
    int[] pi = new int[a.length()];
    for (int i = 1; i < a.length(); i++) {
        for (int j = i; j > 0; j--) {
            if (a.substring(0,j).equals(a.substring(i-j+1,i+1))) {
                pi[i] = j;
                break;
            }
        }
    }
    return pi;
}

该算法的时间复杂度为$O(N^3)$, 在优化该算法前, 我们需了解$\pi[i]$的涵义, $\pi[i]$共有两种涵义:

  • $\pi[i]$表示最长相等前后缀的长度
  • 若$a[\pi[i]] == a[i+1]$, 则$\pi[i+1] = \pi[i]+1$, 因此$\pi[i]$表示$\pi[i+1]$的前缀字符串的末尾字符位置

计算$\pi{i+1}$时, 我们已知$\pi[i]$的值, 而相邻的前缀函数最多增加1, 因此分为以下情况:

  • 若$a[i+1] == a[\pi[i]]$: $\pi[i+1] = \pi[i] + 1$
  • 若$a[i+1] != a[\pi[i]]$: 寻找仅次于$\pi[i]$的第二长度j, 且j必须保证相等前缀和性质($a[0 \ldots j-1] == a[i-j+1 \ldots i]$). 若存在坐标j, 则比较$a[i+1]$和$a[j]$, 若相等, 则$\pi[i+1] = j+1$; 若不存在j, 则寻找仅次于j的第二长度$j_2$, 如此循环, 直到j为0.
int[] prefix(String a) {
    int[] pi = new int[a.length()];
    for (int i = 1; i < a.length(); i++) {
        int j = pi[i-1];
        while (j > 0 && a.charAt(i) != a.charAt(j)) j = pi[j-1];
        if (a.charAt(i) == a.charAt(j)) j++;
        pi[i] = j;
    }
    return pi;
}

该算法的时间复杂度为$O(N)$.

3.4 KMP Implementation

在进行真正的匹配前, 需计算T中每个元素的next值, 即当前字符与S不匹配时, 公共字符串的最长相等前后缀长度. 假设S[i] != T[j], 则next[j]为$pi[i-1]$, 规定next[0] = -1, next[1] = 0. 

int indexOf(String s, String t) {
    int i = 0, j = 0;
    int[] next = getNext(t);
    while (i < s.length() && j < t.length()) {
        if (s.charAt(i) == t.charAt(j)) { // matched
            i++;
            j++;
        } else if (next[j] == -1) { // unmatched, and no available pi
            i++;
        } else { // unmatched, move to next pi
            j = next[j];
        }
    }
    return j == t.length() ? i - j : -1;
}
    
int[] getNext(String a) {
    int[] next = new int[a.length()];
    next[0] = -1;
    int i = 2, j = 0; // j = next[i-1]
    while (i < a.length()) {
        if (a.charAt(i-1) == a.charAt(j)) { // matched, pi[i] = pi[i-1] + 1
            next[i++] = ++j;
        } else if (j > 0) { // unmatched, search for second longest pi 
            j = next[j];
        } else {
            next[i++] = 0; // unmatched, and no available pi
        }
    }
    return next;
}

3.5 DFA Simulation

从另一个角度来看, KMP算法课看做一个DFA(Deterministic finite automaton, 确定性有限状态自动机):

  • $Q$: 一个有限状态集合
  • $\sum$: 一个有限的非空输入字符集
  • $\delta$: 变换函数
  • $q_0$: 开始状态
  • $F$: 接受状态集合

对于字符串匹配, DFA可描述为:

  • $Q$:若字符串T长度为N, 则状态集大小为N
  • $\sum$: ASCII字符
  • $\delta$: KMP实现的状态转换函数

假设T为"ABABAC", DFA的状态转换图如下: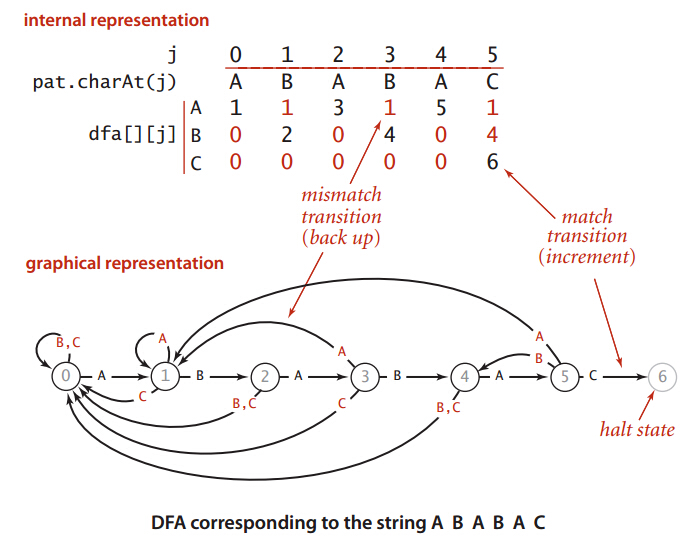
Binary Heap

为构建一个DFA, 我们需要一个dfa二维数组, 每一行对应一种输入(ASCII), 每一列对应一种状态([0,N-1]), 若dfs[X][Y] = Z, 表示DFA当前状态为Y, 当前输入为X, 状态应切换为Z. 构造DFA的代码如下:

public KMP(char[] T) {
    int m = T.length;
    dfa = new int[128][m];
    dfa[T[0]][0] = 1;
    for (int x = 0, j = 1; j < m; j++) {
        for (int c = 0; c < 128; c++) {
            dfa[c][j] = dfa[c][x]; // Copy mismatch cases.
        }
        dfa[T[j]][j] = j + 1; // Set match case.
        x = dfa[T[j]][x];     // Update restart state.
    }
}

该函数中的j在循环中递增, 因此整个函数实际上从小到大更新每一种状态(每一列)下任意输入字符的状态转换. 假设当前状态为j, 当前输入字符为c, 则存在两种状态转换的情况:

  • c == T[j]: 状态切换为j+1
  • c != T[j]: 状态回退(<j)或维持不变(j)

c == T[j]时可写作dfa[T[j]][j] = j+1; 若c != T[j], 则需找到当前状态的最长相等前缀状态, 假设为x, 则x已输入的字符串与j的后缀字符串相同, 且为最长. 这时可将j的输入字符交给x处理, 也就是dfa[c][j] = dfa[c][x]. 这与上一节的KMP实现相同: 若状态无法前进, 则后退尽量少的字符, 也就是最长相等前后缀.
问题在于如何获得状态j下的最长相等前缀状态x, 上述函数中x = dfa[T[j]][x]负责更新j+1状态的最长相等前缀状态, 可以理解为: 在状态x上输入当前字符T[j], 存在两种可能:

  • 前缀和后缀追加T[j]后, x依然满足相等的前缀, 最长相等前缀的长度增加
  • 前缀和后缀追加T[j]后, x无法构成相等的前缀, 因此状态后退或维持不变

由于状态j之前的状态转换已计算完毕, 且x < j, 因此dfa[T[j]][x]一定返回状态x下输入为T[j]的最长相等前缀状态x', 也就是状态j+1的最长相等前缀状态.