HashMap

1. Hash Collision(哈希冲突)

当key的集合很大时, 根据Birthday Paradox(生日问题)原理, 哈希冲突是不可避免的. 所以必须采取一个哈希避免方法.

2 Hash Resolution

主流的解决方法有两种:

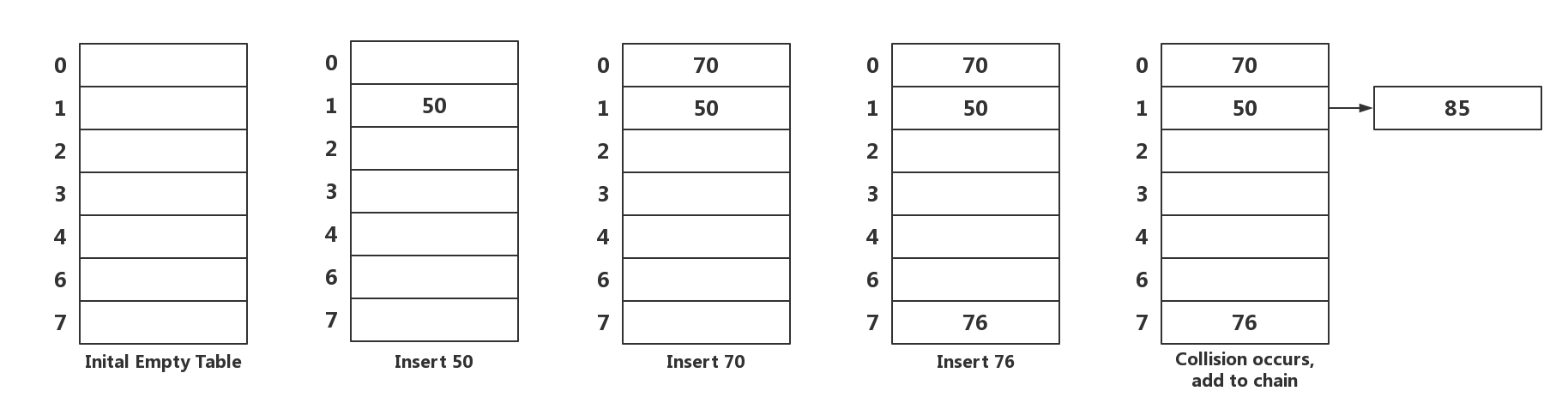
2.1 冲突链表法(Separate Chaining)

使用数组(假设数组名为table)保证读取效率为O(1), 使用hash function得到元素的hash value. hash value % table.length 表示元素在数组中的index. 如果index发生冲突, 该数组元素指向一个chain, chain中的元素拥有相同的index
例如: 现在有一个长度为7的数组, 现有hash value值为50, 70, 76和85需要插入.

2.2 开发地址法(Open addressing)

此方法将所有元素存在hash table中, 并不需要动态申请节点. 所以table的长度必须大于等于元素的个数.

• 插入元素: 如果hash function得出的hash value对应的slot不为空时, 继续进行probe, 直到找到一个空的slot.
• 查找元素: 不断probe直到元素为目标元素或slot为空.
• 删除元素: 由于查找元素时遇到slot为空则说明没有找到, 所以删除时不能将slot置为空, 只能标记该slot为"deleted"状态.

Open Addressing通过probe sequence(探测序列)来实现不断probing, 有以下几种探测序列:

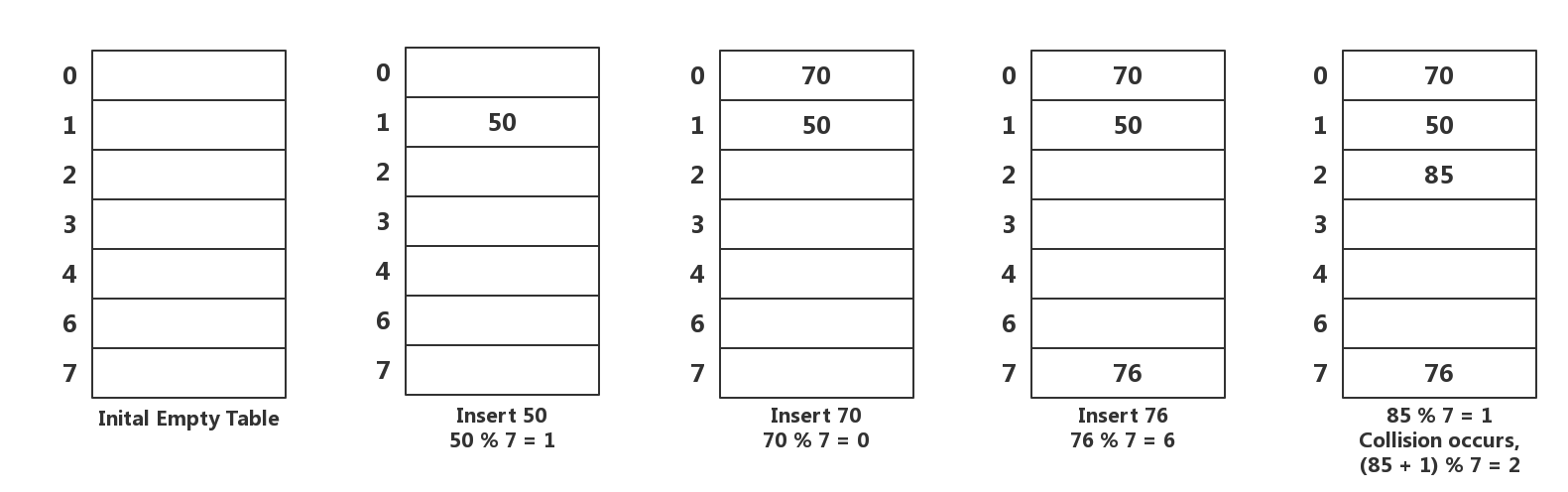
1. Linear Probing(线性探测):
   hash(x) % S
   (hash(x) + 1) % S
   (hash(x) + 2) % S
   (hash(x) + 3) % S
2. Quadratic Probing(二次探测):
   hash(x) % S
   (hash(x) + 1 × 1) % S
   (hash(x) + 2 × 2) % S
   (hash(x) + 3 × 3) % S
3. double hashing probing(双重散列探测):
   hash(x) % S
   (hash(x) + 1 × hash2(x)) % S
   (hash(x) + 2 × hash2(x)) % S
   (hash(x) + 3 × hash2(x)) % S

以Linear Probing为例, 现在有Hash value为50, 70, 76, 85

2.3 两种方式的优缺点对比

方式	Cache Performance	Space Wasting	need to know the number of elements	Search Performance	difficulty of implementation	demand of hash function
Separate Chaining	慢	多	不需要	慢	简单	低
Open Addressing	快	少	需要	快	较难	高

3. HashMap

3.1 HashMap结构

Java的HashMap采用了Separate Chaining作为Hash Collision的解决方法. 当table中某个slot所连的chain过长时, 将chain转化为Red-Black Tree, 用于提高搜索元素的效率.
HashMap采用一个"负载因子"(load factor)来控制HashMap中的元素数量. 当有元素插入HashMap的slot时:

• 已占用的slot数量 / 总slot数 >= load factor, 则需要对table进行扩容
• 已占用的slot数量 / 总slot数 < load factor, 则不需要对table进行扩容

假设table中有n个slot, 那么table的threshold会小于等于n, 这样装入table中的元素

3.2 重要参数

/* HashMap最重要的部分, 用于存放Key和Value. 长度永远为2的次方大小 */
transient Node<K,V>[] table;

/* table所能装载的最大数量, 如果size >= threshold, 则需要扩充table */
int threshold;

/* 默认的初始化table大小 */
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; /* 16 */

/* table所能达到的最大大小 */
static final int MAXIMUM_CAPACITY = 1 << 30;

/* HashMap修改的次数 */
transient int modCount;

/* HashMap当前所拥有的元素数量 */
transient int size;

3.3 table的组成单位 - Node

/* 存储一组Key和Value的基本单元, 链表结构, 一个Node可以后面跟多个Node */
static class Node<K,V> implements Map.Entry<K,V> {
  final int hash;
  final K key;
  V value;
  Node<K,V> next;

  /**
   * 初始化函数
   * @param hash  key的hash值
   * @param key
   * @param value
   * @param next  Node可组成链表形式
   */
  Node(int hash, K key, V value, Node<K,V> next) {
    this.hash = hash;
    this.key = key;
    this.value = value;
    this.next = next;
  }

  public final K getKey()    { return key; }
  public final V getValue()    { return value; }
  public final String toString() { return key + "=" + value; }

  public final int hashCode() {
    return Objects.hashCode(key) ^ Objects.hashCode(value);
  }

  public final V setValue(V newValue) {   // 设置value, 并获得被替换的value
    V oldValue = value;
    value = newValue;
    return oldValue;
  }

  public final boolean equals(Object o) {
    if (o == this)
      return true;
    if (o instanceof Map.Entry) {
      Map.Entry<?,?> e = (Map.Entry<?,?>)o;
      if ( Objects.equals(key, e.getKey()) && Objects.equals(value, e.getValue()) )
        return true;
    }
    return false;
  }
}

3.4 table扩容函数(也用于初始化)

final Node<K,V>[] resize() {
  /* oldTab: 需要被扩容的table
   * oldCap: table的长度
   * oldThr: 当前的threshold
   */
  Node<K,V>[] oldTab = table;
  int oldCap = (oldTab == null) ? 0 : oldTab.length;
  int oldThr = threshold;
  int newCap, newThr = 0;

  /* 根据当前table的长度和threshold决定新的table的长度和新的threshold 
   * 设置newCap和newThr的流程:
   * 1. oldCap > 0:
   *    1. oldCap已经达到最大值, 退出resize()
   *    2. newCap和newThr都扩充两倍
   * 2. oldThr > 0 && oldCap == 0: oldCap = oldThr, newThr默认为0
   * 3. oldThr == 0 && oldCap == 0: 都设置为默认值
   * 4. newThr == 0: 设置为newCap * loadFactor
   */ 
  if (oldCap > 0) {
    if (oldCap >= MAXIMUM_CAPACITY) {   
      threshold = Integer.MAX_VALUE;  /* 将threshold设置为最大值, 这样能使用table剩余的slot */
      return oldTab;  /* 无法扩大table, 直接退出 */
    }
    /* threshold变为table长度的两倍 */
    else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY)
      newThr = oldThr << 1;
  }
  else if (oldThr > 0)  /* 根据当前的threshold决定新的table的长度 */
    newCap = oldThr;
  else {  /* 如果HashMap<>()中没有设定threshold, threshold默认为0; 如果HashMap第一次使用, oldCap也为0 */ 
    newCap = DEFAULT_INITIAL_CAPACITY;
    newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
  }
  if (newThr == 0) {  /* 如果oldThr大于0, 则newThr会成为默认0, 必须重新设置 */
    float ft = (float)newCap * loadFactor;
    newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? (int)ft : Integer.MAX_VALUE);
  }

  /* 初始化新的table, 长度为newCap, threshold为newThr */
  threshold = newThr;
  @SuppressWarnings({"rawtypes","unchecked"})
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
  table = newTab;

  /* 将oldTab中的Node移动到newTab中
   * 步骤如下:
   * 1. 将oldTab中不为null的Node赋值给e, 并将oldTab中的Node置为null
   * 2. 若e不为链表, 则直接移动e到newTab
   * 3. 若e是链表, 则分两种情况
   *  1. e开头的链表中节点不需重新定位, 放入loHead开头的链表中
   *  2. e开头的链表中节点需要重新定位, 放入hiHead开头的链表中
   */
  if (oldTab != null) {
    for (int j = 0; j < oldCap; ++j) {  /* 遍历旧的table, 将所有Node移到新的table中 */
      Node<K,V> e;
      if ((e = oldTab[j]) != null) {  /* e是不为null的oldTab[j] */
        oldTab[j] = null;       /* 将oldTab上的元素置为null */
        if (e.next == null)
          newTab[e.hash & (newCap - 1)] = e;
        else if (e instanceof TreeNode)
          ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
        else {
          Node<K,V> loHead = null, loTail = null;
          Node<K,V> hiHead = null, hiTail = null;
          Node<K,V> next;
          do {
            next = e.next;
            if ((e.hash & oldCap) == 0) {   /* e不需要重新定位 */
              if (loTail == null)
                loHead = e;
              else
                loTail.next = e;
              loTail = e;
            } else {            /* e需要重新定位 */
              if (hiTail == null)
                hiHead = e;
              else
                hiTail.next = e;
              hiTail = e;
            }
          } while ((e = next) != null);
          if (loTail != null) {         /* loHead开头的链表不需要重新定位 */
            loTail.next = null;
            newTab[j] = loHead;       /* 直接移动到newTab中的原位置 */
          }
          if (hiTail != null) {
            hiTail.next = null;
            newTab[j + oldCap] = hiHead;  /* 移动时需要加上偏移量oldCap, 因为newTab == 2 * oldTab */
          }
        }
      }
    }
  }
  return newTab;
}

4. HashMap初始化

4.1 默认的HashMap()

static final float DEFAULT_LOAD_FACTOR = 0.75f;

public HashMap() {
  this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}

4.2 带参数的HashMap()

static final int MAXIMUM_CAPACITY = 1 << 30;

public HashMap(int initialCapacity) {
  this(initialCapacity, DEFAULT_LOAD_FACTOR);
}

public HashMap(int initialCapacity, float loadFactor) {
  /* 参数查错 */
  if (initialCapacity < 0)
    throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity);
  if (initialCapacity > MAXIMUM_CAPACITY)
    initialCapacity = MAXIMUM_CAPACITY;
  if (loadFactor <= 0 || Float.isNaN(loadFactor))
    throw new IllegalArgumentException("Illegal load factor: " + loadFactor);
  
  /* 初始化 */
  this.loadFactor = loadFactor;
  this.threshold = tableSizeFor(initialCapacity);
}

static final int tableSizeFor(int cap) {
  /* 返回一个2的n次方作为HashMap的初始化大小, 不能超过MAXIMUM_CAPACITY
   * 例如: 10(1010), 返回16(10000)
   */
  int n = cap - 1;
  n |= n >>> 1;
  n |= n >>> 2;
  n |= n >>> 4;
  n |= n >>> 8;
  n |= n >>> 16;
  return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}

5. put()

public V put(K key, V value) {
  return putVal(hash(key), key, value, false, true);
}

static final int hash(Object key) { /* 获得key的hash值 */
  int h;
  return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

/**
 * 实现了Map.put
 * @param hash  key的hash值
 * @param key   
 * @param value 
 * @param onlyIfAbsent 若为true, 不改变已存在的value
 * @param evict 若为false, if false, the table is in creation mode.
 * @return 若slot中已有元素, 则返回该元素; 若为空, 则返回null
 */
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
  /* tab: 当前table 
   * p:   key指向的Node元素
   * n:   table的长度
   * i:   key在table中的位置
   */
  Node<K,V>[] tab;  
  Node<K,V> p;
  int n, i;
  if ((tab = table) == null || (n = tab.length) == 0)
    n = (tab = resize()).length;

  /* 插入时有两种情况:
   * 1. key所指向的slot上没有Node, 直接放置即可
   * 2. key所指向的slot上已经有Node, 需要在链表中操作
   */
  if ((p = tab[i = (n - 1) & hash]) == null)
    tab[i] = newNode(hash, key, value, null);   /* slot上没有Node, 直接放置 */
  else {  /* slot上已有Node, 需要对slot上的链表进行操作 */
    /* e: 要被替换的Node
     * k: 表示p的key值   
     */
    Node<K,V> e;
    K k;

    /* 已经找到了插入位置的slot, 分3种情况:
     * 1. slot中的Node就是要替换的Node
     * 2. 从slot中的链表中找到要替换的Node
     *    1. 试图找到要替换的Node
     *    2. 查找目标Node时统计链表长度, 检查链表是否因过长而需要转化为Tree结构
     * 3. 链表中没有找到要替换的Node, 在链表末尾添加该Node
     */
    if ( p.hash == hash && ( (k = p.key) == key || (key != null && key.equals(k)) ) )
      e = p;  /* 直接将slot中的e替换为p */ 
    else if (p instanceof TreeNode)
      e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
    else {    /* 试图在链表中寻找要被替换的Node */
      for (int binCount = 0; ; ++binCount) {  /* binCount用于统计链表长度 */
        if ((e = p.next) == null) {     /* 到达链表末尾, 说明未找到可替换的Node, 直接在尾部添加即可 */
          p.next = newNode(hash, key, value, null);
          /* 链表过长会影响了搜索效率, 判断是否将该slot上的链表转化为Red-Black Tree */
          if (binCount >= TREEIFY_THRESHOLD - 1)
            treeifyBin(tab, hash);
          break;
        }
        /* 在链表上找到了需要替换的Node, 退出链表搜索 */
        if (e.hash == hash && ( (k = e.key) == key || (key != null && key.equals(k)) ) )
          break;
        p = e;
      }
    }
    /* 若e != null, 说明e就是需要被替换的Node */
    if (e != null) { // existing mapping for key
      V oldValue = e.value;
      if (!onlyIfAbsent || oldValue == null)
        e.value = value;
      afterNodeAccess(e); /* 为LinkedHashMap设计的处理函数, HashMap中为空 */
      return oldValue;
    }
  }
  ++modCount;
  if (++size > threshold)   /* 检查table是否需要扩容 */
    resize();
  afterNodeInsertion(evict);  /* 为LinkedHashMap设计的处理函数, HashMap中为空 */
  return null;
}

// 创建一个Node
Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) {
  return new Node<>(hash, key, value, next);
}

6. get()

public V get(Object key) {
  Node<K,V> e;
  return (e = getNode(hash(key), key)) == null ? null : e.value;
}

/** 
 * 实现了Map.get()
 * @param hash  hash for key
 * @param key   the key
 * @return    node or null
 */
final Node<K,V> getNode(int hash, Object key) {
  /* tab:   当前table
   * first:   hash所指向的slot位置
   * e:     first.next
   * n:     table的长度
   * k:     first.key 或 e.key
   */
  Node<K,V>[] tab; 
  Node<K,V> first, e; 
  int n; 
  K k;

  /* 总体上分两种情况:
   * 1. hash指向的slot存在Node
   *    1. slot上的Node就是查找的Node, 返回first即可
   *    2. first不是要查找的元素, 需要搜索整条链表
   *      1. 链表上的某个Node的key与查找的key相同, 返回e(该节点)
   *      2. 否则返回null
   * 2. slot中没有Node, 直接返回null
   */
  if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) {
    /* 先查看slot上的Node */ 
    if (first.hash == hash && ((k = first.key) == key || (key != null && key.equals(k))))
      return first;
    /* 再在链表上查找 */
    if ((e = first.next) != null) {
      if (first instanceof TreeNode)  /* 链表过长导致已经转换为Tree结构 */
        return ((TreeNode<K,V>)first).getTreeNode(hash, key);
      do {  /* slot上依旧是链表, 循环查找 */
        if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
          return e;   /* got it */
      } while ((e = e.next) != null);
    }
  }
  return null;
}

7. remove()

public V remove(Object key) {
  Node<K,V> e;
  return (e = removeNode(hash(key), key, null, false, true)) 
       == null ? null : e.value;
}

/**
 * 实现Map.remove()
 * @param hash  key的hash值
 * @param key
 * @param value 若matchValue == True, 则除了匹配key之外还需要匹配value
 * @param matchValue
 * @param movable if false do not move other nodes while removing
 * @return node or null
 */
final Node<K,V> removeNode(int hash, Object key, Object value, boolean matchValue, boolean movable) {
  /* tab: 当前table
   * p:   key的hash指向的slot中的Node
   * n:   table的长度
   * index: p在table中的位置
   */
  Node<K,V>[] tab; 
  Node<K,V> p; 
  int n, index;

  /* 删除前需要先查找该key, 查找的过程与get()类似 */
  if ((tab = table) != null && (n = tab.length) > 0 &&
    (p = tab[index = (n - 1) & hash]) != null) {
    Node<K,V> node = null, e;   /* node为要被删的Node, e为p.next */
    K k; /* k: key */
    V v; /* v: value */
    if (p.hash == hash &&
      ((k = p.key) == key || (key != null && key.equals(k))))
      node = p;
    else if ((e = p.next) != null) {
      if (p instanceof TreeNode)
        node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
      else {
        do {
          if (e.hash == hash &&
            ((k = e.key) == key ||
              (key != null && key.equals(k)))) {
            node = e;
            break;
          }
          p = e;
        } while ((e = e.next) != null);
      }
    }
    /* node != null说明查找到被删除的节点 */
    if (node != null && (!matchValue || (v = node.value) == value ||
                (value != null && value.equals(v)))) {
      if (node instanceof TreeNode)
        ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
      else if (node == p) /* node为slot中的Node */
        tab[index] = node.next;
      else        /* node为链表中的Node */
        p.next = node.next;
      ++modCount;
      --size;
      afterNodeRemoval(node);
      return node;
    }
  }
  return null;
}