1. Introduction

Binary search tree(BST, 二叉搜索树)是一种binary tree(二叉树)的树型数据结构, 定义如下:

  • 若BST的左子树不为空, 则其左子树上所有节点的权值均小于其根节点的权值
  • 若BST的右子树不为空, 则其右子树上所有节点的权值均小于其根节点的权值
  • BST的左右子树均为BST
  • 空树也是BST

1.1 BST Traversal

BST的inorder traversal(中序遍历)的序列为非降序序列, 时间复杂度为$O(n)$(BST的节点数为n)

1.2 Minimum and Maximum

由BST的性质可得, BST左链的顶点为最小值, 右链的顶点为最大值, 时间复杂度为$O(n)$(BST的节点数为n)

1.3 Insert an Element

假设BST的根节点为o, 插入的新节点值为v, 则插入元素时分为以下几种情况:

  • 若o为空, 直接返回值为v的新节点
  • 若o的权值等于v, 则不添加新的节点
  • 若o的权值大于v, 则在o的左子树插入权值为v的节点
  • 若o的权值小于v, 则在o的右子树插入权值为v的节点

1.4 Delete an Element

假设BST的根节点为o, 删除一个值为v的节点, 首先需要在BST中找到权值为v的节点:

  • 若o为空, 则BST中不存在权值为v的节点, 无需删除
  • 若o的权值等于v, 则删除当前节点o
  • 若o的权值大于v, 则在o的左子树删除权值为v的节点
  • 若o的权值小于v, 则在o的右子树删除权值为v的节点

2. Implementation

2.1 Query Element

查找元素时, 只需根据情况判断需向左子树或右子树走, 每次判断都会缩小查找范围, 从而提高查找效率. 假设目标值为val, 从根节点出发:

  1. 若当前节点为空, 则查找失败
  2. 若当前节点不为空, 对比节点值与目标值
    • 若$val = node.val$, 则查找成功
    • 若$val < node.val$, 则查找左子树
    • 若$val > node.val$, 则查找右子树

最好的情况下, BST与二分查找类似, 从根节点到叶子节点的高度为$\log_2 n$, 因此时间复杂度为$O(\log_2 n)$; 最坏情况下, BST会变为一个链表, 即只有左子树或右子树, 退化为顺序查找, 因此时间复杂度为$O(n)$.

2.2 Insert Element

插入操作与查找操作的步骤类似, 假设插入值为val, 从根节点出发:

  1. 若当前节点为空, 则创建一个值为val的节点
  2. 若当前节点不为空, 比较节点值和插入值:
    • 若$val < node.val$, 则插入左子树
    • 若$val > node.val$, 则插入右子树

由于BST不允许重复节点, 因此若插入值已存在于BST中, 则直接返回.

2.3 Delete Element

在BST中删除元素需先找到被删除节点, 再执行删除操作. 被删除节点可分为三种情况:

  1. 被删除节点的左子树为空, 则让右子树代替被删除节点
  2. 被删除节点的右子树为空, 则让左子树代替被删除节点
  3. 被删除节点的左右子树均不为空, 则让immediate predecessor/successor(直接前驱或直接后继, 也就是小于被删除节点值的最大值, 或大于被删除节点值的最小值)代替被删除节点

BST删除元素的步骤如下, 从根节点出发:

  1. 若当前元素为空, 则返回空
  2. 若$val < node.val$, 则从左子树搜索并删除, 之后更新node.left
  3. 若$val > node.val$, 则从右子树搜索并删除, 之后更新node.right
  4. 若$val = node.val$, 则当前节点为被删除节点:
    • 若当前节点的左子树为空, 则让右子树代替当前节点, 返回右子树
    • 若当前节点的右子树为空, 则让右子树代替当前节点, 返回左子树
    • 若当前节点的左右子树均不为空, 则将左子树转移到右子树最左侧叶子节点的位置上, 并让右子树代替当前节点, 返回右子树

3. Leetcode

95. Unique Binary Search Trees II

Problem Description

Given an integer n, return all the structurally unique BST's (binary search trees), which has exactly n nodes of unique values from 1 to n. Return the answer in any order.

Example 1: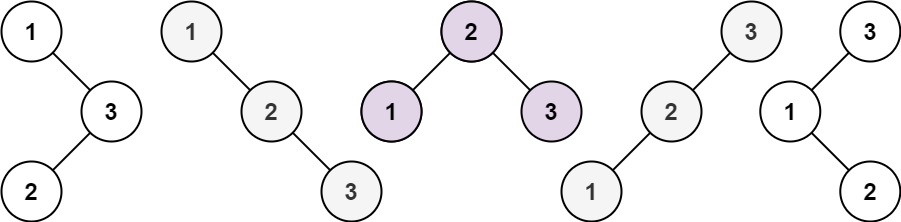
Unique Binary Search Trees II

Input: n = 3
Output: [[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

Solution

class Solution {
    public List<TreeNode> generateTrees(int n) {
        return helper(1, n);
    }

    private List<TreeNode> helper(int l, int r) {
        List<TreeNode> res = new ArrayList<>();
        if (l > r) {
            res.add(null);
            return res;
        };
        for (int i = l; i <= r; i++) {
            List<TreeNode> ls = helper(l, i-1), rs = helper(i+1, r);
            for (TreeNode left: ls) {
                for (TreeNode right: rs) {
                    TreeNode node = new TreeNode(i);
                    node.left = left;
                    node.right = right;
                    res.add(node);
                }
            }
        }
        return res;
    }
}

98. Validate Binary Search Tree

Problem Description

Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:

  • The left subtree of a node contains only nodes with keys less than the node's key.
  • The right subtree of a node contains only nodes with keys greater than the node's key.
  • Both the left and right subtrees must also be binary search trees.

Example 1: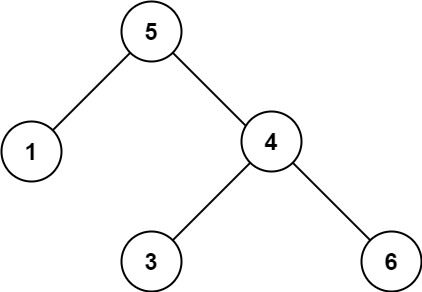
Validate Binary Search Tree

Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Solution

class Solution {
    public boolean isValidBST(TreeNode root) {
        return helper(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    private boolean helper(TreeNode root, long min, long max) {
        if (root == null) return true;
        if (root.val < min || root.val > max) return false;
        return helper(root.left, min, (long)root.val-1) && helper(root.right, (long)root.val+1, max);
    }
}

669. Trim a Binary Search Tree

Problem Description

Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer.

Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.

Example 1: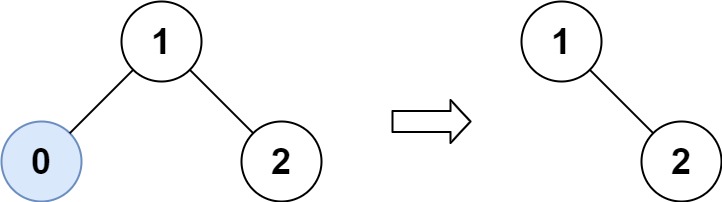
Trim a Binary Search Tree

Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]

Solution

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) return null;
        TreeNode l = trimBST(root.left, low, high), r = trimBST(root.right, low, high);
        if (root.val < low || root.val > high) {
            return l == null ? r : l;
        }
        root.left = l;
        root.right = r;
        return root;
    }
}

235. Lowest Common Ancestor of a Binary Search Tree

Problem Description

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: "The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself)."

Example 1: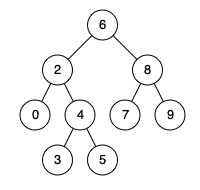
Lowest Common Ancestor of a Binary Search Tree

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Solution

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) return root;
        if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
        if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
        return root;
    }
}

450. Delete Node in a BST

Problem Description

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.
Basically, the deletion can be divided into two stages:

  1. Search for a node to remove.
  2. If the node is found, delete the node.

Example 1: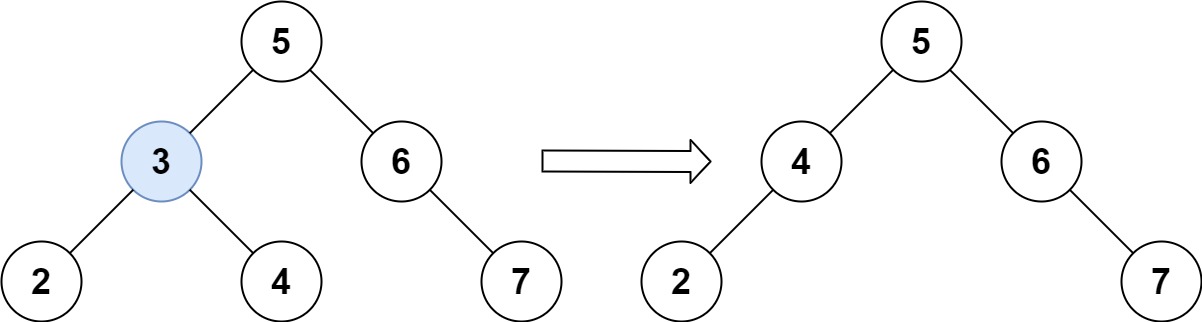
Delete Node in a BST

Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.

Solution

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;
        if (root.val == key) {
            TreeNode l = root.right;
            if (l == null) return root.left;
            while (l.left != null) {
                l = l.left;
            }
            l.left = root.left;
            return root.right; 
        }
        if (root.val < key) {
            root.right = deleteNode(root.right, key);
        } else {
            root.left = deleteNode(root.left, key);
        }
        return root;
    }
}

230. Kth Smallest Element in a BST

Problem Description

Given the root of a binary search tree, and an integer k, return the $k^{th}$ smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:
Kth Smallest Element in a BST

Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Solution

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Stack<TreeNode> stack = new Stack<>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if (--k == 0) break;
            root = root.right;
        }
        return root.val;
    }
}

1373. Maximum Sum BST in Binary Tree

Problem Description

Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

  • The left subtree of a node contains only nodes with keys less than the node's key.
  • The right subtree of a node contains only nodes with keys greater than the node's key.
  • Both the left and right subtrees must also be binary search trees.

Example 1: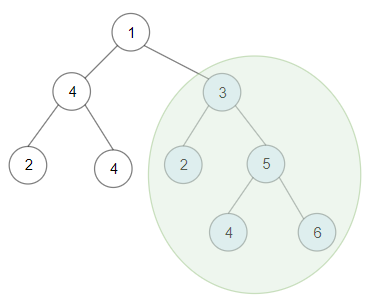
Maximum Sum BST in Binary Tree

Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Solution

class Solution {
    class Node {
        public int min, max, sum;
        public Node(int min, int max, int sum) {
            this.min = min;
            this.max = max;
            this.sum = sum;
        }
    }

    private int res = 0;

    public int maxSumBST(TreeNode root) {
        postorder(root);
        return res;
    }

    private Node postorder(TreeNode node) {
        if (node == null) {
            return new Node(Integer.MAX_VALUE, Integer.MIN_VALUE, 0);
        }
        Node l = postorder(node.left), r = postorder(node.right);
        if (l == null || r == null || node.val <= l.max || node.val >= r.min) {
            return null;
        }
        int sum = node.val + l.sum + r.sum;
        res = Math.max(res, sum);
        return new Node(Math.min(l.min, node.val), Math.max(r.max, node.val), sum);
    }
}

272. Closest Binary Search Tree Value II

Problem Description

Given the root of a binary search tree, a target value, and an integer k, return the k values in the BST that are closest to the target. You may return the answer in any order.
You are guaranteed to have only one unique set of k values in the BST that are closest to the target.

Example 1: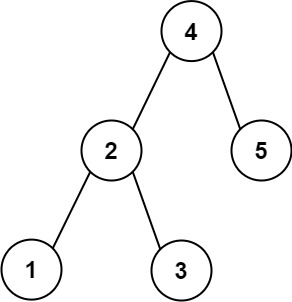
Closest Binary Search Tree Value

Input: root = [4,2,5,1,3], target = 3.714286, k = 2
Output: [4,3]

Solution

class Solution {
    private Deque<Integer> deque = new ArrayDeque<>();

    public List<Integer> closestKValues(TreeNode root, double target, int k) {
        inorder(root, target, k);
        List<Integer> res = new ArrayList<>();
        while (!deque.isEmpty()) {
            res.add(deque.pollFirst());
        }
        return res;
    }

    private void inorder(TreeNode node, double target, int k) {
        if (node == null) return;
        inorder(node.left, target, k);
        double diff = Math.abs(node.val - target);
        if (deque.size() == k) {
            double d1 = Math.abs(deque.peekFirst() - target), d2 = Math.abs(deque.peekLast() - target);
            if (diff < d1 || diff < d2) {
                if (d1 < d2) deque.pollLast();
                else deque.pollFirst();
                deque.offerLast(node.val);
            }
        } else {
            deque.offerLast(node.val);
        }
        inorder(node.right, target, k);
    }
}