1. Bottom-Up Parsing

从parse tree角度来说, Bottom-up parser从叶子节点出发, 不断向上收缩, 直到root. 其中, scanner返回的每个单词都是一个叶子节点, 这些叶子节点构成了parse tree的下边缘. 为构建一个derivation, parser需要根据语法和parse tree中的节点来构成nonterminal symbol. parse tree中的叶子节点表示scanner返回的单词, 叶子节点之上的节点表示可推导出的语法, parse将沿着已完成的parse tree上边缘不断推断, 直到回到根节点.
假设存在一个production: $A \rightarrow \beta$, 在parse tree的上边缘已经找到$\beta$, 其右端位于k, 那么parser可将$\beta$替换为A, 从而创建新的上边缘. 若有效推导中, 需要在位置k用A替换$\beta$, 那么$(A \rightarrow \beta, k)$这种推导称为handle, 用A替换$\beta$称为reduction, 可减少上边缘的symbol数量.
Buttom-up parser中最关键的问题在于寻找handle, 并重复一个简单的过程: parser在parse tree的上边缘找到一个handle $(A \rightarrow \beta, k)$, 并将位置k的$\beta$替换为A, 直到出现以下两种情况之一:

  1. parse tree的上边缘只有一个节点, 该节点为goal symbol, 表示语法分析成功
  2. 无法找到handle, 表示语法分析失败

Button-up parser从goal symbol出发, 向最终语句方向推导, parser会按照逆向推导各个步骤:
$$
Goal = \gamma_1 \rightarrow \gamma_2 \rightarrow \cdots \rightarrow \gamma_{n-1} \rightarrow \gamma_{n} = sentence
$$

Buttm-up parser会先发现$\gamma_i \rightarrow \gamma_{i+1}$, 然而才发现$\gamma_{i-1} \rightarrow \gamma_i$, 因为parse tree是树型结构, 在匹配$\gamma_i$之前, parser必须在parse tree的上边缘发现$\gamma_i$对应的节点. Scanner按照从左向右的顺序返回归类后的单词, 为使parser的推导方向与scanner的扫描方向一致吗, parser需要将寻找最右推导, 并首先匹配最左叶子节点, 最后匹配最右叶子节点. 这样当parser需要更多信息来推导时, 可直接调用scanner来获取单词.
LR(1)作为buttom-up parser中的一种, 使用一个前瞻符号来寻找从$\gamma_i$到$\gamma_{i-1}$的handle, L表示从左(Left)到右扫描, R表示反向(Reverse)最右推导, 1表示一个前瞻符号.

1.1. The LR(1) Parsing Algorithm

LR(1) parser可借助Action和Goto两个表来快速定位handle, 算法如下:

push $;
push start state, $s_0$;
word $\leftarrow$ NextWord( );
while (true)
  state $\leftarrow$ top of stack;
  if Action[state, word] = "$\textit{reduce} \ A \rightarrow \beta$"
    pop 2 × |$\beta$| symbols;
    state $\leftarrow$ top of stack;
    push A;
    push Goto[state, A];
  else if Action[state, word] = "$\textit{shift} \ s_i$"
    push word;
    push $s_i$;
    word $\leftarrow$ NextWord( );
  else if Action[state, word] = "$accept$"
    break;
  else
    Fail( );
report success; /* executed break on "accept" case */

上述算法存在四种情况:

  1. 当LR(1)找到一个handle $(A \rightarrow \beta, k)$时, 将当前矩形中位置k处的$\beta$替换为A, 也就是reduction
  2. 当LR(1)无法找到handle, 则将单词和状态加入栈中
  3. 语法推导成功
  4. 语法推导失败

其中, 前瞻符号表示production后紧接的第一个terminal symbol, 也就是算法中不存放于栈中的第一个单词. 当LR(1) parser无法找到handle时会不断将单词压入栈中, 直到找到一个handle并进行reduction. 以括号语法为例:

1 ${Goal} \rightarrow {List}$
2 ${List} \rightarrow {List} \ {Pair}$
3     $| \ Pair$
4 ${Pair} \rightarrow \underline{(} \ {Pair} \ \underline{)}$
5     $| \ \underline{(} \ \underline{)}$

以下是Action表和Goto表: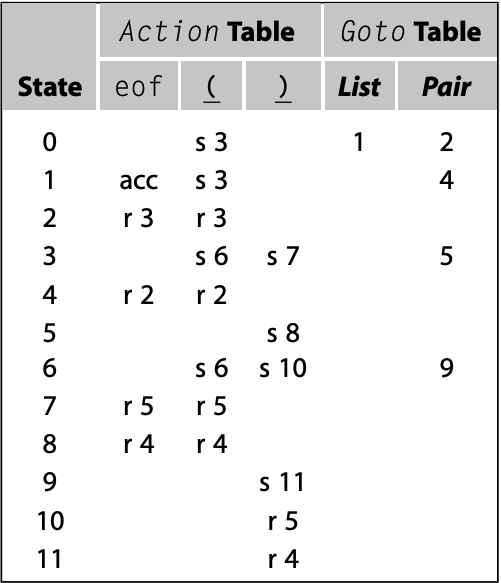
Action and Goto Tables

以下是LR(1) parser处理输入串$\underline{(}\underline{)}$的操作序列:

Iteration State word Stack Handle Action
initial - \underline{(} \$ 0 - -
1 0 \underline{(} \$ 0 - shift 3
2 3 \underline{(} \$ 0 \underline{(} 3 - shift 7
3 7 eof \$ 0 \underline{(} 3 \underline{)} 7 $\underline{(}$ $\underline{)}$ reduce 5
4 2 eof \$ 0 Pair 2 Pair reduce 3
5 1 eof \$ 0 List 1 List accept

表中第一行为初始状态, 从第二行开始进入while循环. 第一次循环栈中没有任何handle, 将$\underline{(}$加入到栈中; 第二次循环栈中依然没有任何handle, 将$\underline{)}$移入栈中; 第三次循环栈中存在handle: $\langle \text{Pair} \rightarrow \underline{(} \ \underline{)}, eof \rangle$并进行reduce; 第四次循环stack中存在handle: $\langle \text{List} \rightarrow \text{Pair}, eof \rangle$并进行reduce; 第五次循环stack存在handle: $\langle \text{Goal} \rightarrow \text{Goal}, eof \rangle$. Parser需要使用两个shift和三个reduce操作, 花费的时间与输入字符串长度成正比. 以下是输入串为$\underline{(} \ \underline{(} \ \underline{) \ }\underline{)} \ \underline{(} \ \underline{)}$的操作序列:

Iteration State word Stack Handle Action
initial - $\underline{(}$ \$ 0 - -
1 0 $\underline{(}$ \$ 0 - shift 3
2 3 $\underline{(}$ \$ 0 $\underline{(}$ 3 - shift 6
3 6 $\underline{)}$ \$ 0 $\underline{(}$ 3 $\underline{(}$ 6 - shift 10
4 10 $\underline{)}$ \$ 0 $\underline{(}$ 3 $\underline{(}$ 6 $\underline{)}$ 10 $\underline{(} \underline{)}$ reduce 5
5 5 $\underline{)}$ \$ 0 $\underline{(}$ 3 Pair 5 - shift 8
6 8 $\underline{(}$ \$ 0 $\underline{(}$ 3 Pair 5 $\underline{)}$ 8 $\underline{(}$ Pair $\underline{)}$ reduce 4
7 2 $\underline{(}$ \$ 0 Pair 2 Pair reduce 3
8 1 $\underline{(}$ \$ 0 List 1 - shift 3
9 3 $\underline{)}$ \$ 0 List 1 \underline{(} 3 - shift 7
10 7 eof \$ 0 List 1 \underline{(} 3 \underline{)} 7 $\underline{(} \underline{)}$ reduce 5
11 4 eof \$ 0 List 1 Pair 4 List Pair reduce 2
12 1 eof \$ 0 List 1 List accept

当输入错误字符串时, 如$\underline{(} \ \underline{)} \ \underline{)}$, 其操作序列如下:

Iteration State word Stack Handle Action
initial - $\underline{(}$ \$ 0 - -
1 0 $\underline{(}$ \$ 0 - shift 3
2 3 $\underline{)}$ \$ 0 $\underline{(}$ 3 - shift 7
3 7 $\underline{)}$ \$ 0 $\underline{(}$ $\underline{)}$ 7 - error

前两次迭代与之前相同, 第三次迭代Action表中对应项不为shift, reduce或accpet, 因此判定为error. 当表项中无效时, LR(1) parser即可认为语法错误. 这种性质让parser可将错误定位到某个具体位置, 利用上下文信息和语法知识, 可构建出错误诊断信息.

1.2 Build LR(1) Tables

为构建Action和Goto表, LR(1) parser需要构建一个handle-recognizing automation(句柄识别自动机)的模型来填充表格, 这一模型叫做canonical collection of sets of LR(1) items(LR(1)项集的规范族), 表示parser中所有可能状态之间的转移. Action和Goto表将所有潜在handle信息都保存在表中, 并将潜在handle称为LR(1) item, 表示为$[A \rightarrow \beta \bullet \gamma, a]$, 其中, $A \rightarrow \beta\gamma$为production, $\bullet$表示栈顶的位置, a为前瞻符号, 也可理解为FOLLOW(A). 一个production的所有item集合称为$CC_i$, 所有$CC_i$集合称为canonical collection, 表示为$CC = \{CC_0, CC_1, CC_2, \cdots, CC_n\}$.
对于production $A \rightarrow \beta\gamma$和前瞻符号a来说, 可产生三种不同的item, 且每个item都有不同的解释:

  1. $[A \rightarrow \bullet \beta \gamma]$: 该item并没有读取任何单词, 但A作为一种可能的reduce等待验证
  2. $[A \rightarrow \beta \bullet \gamma]$: 该item已读取到$\beta$, 说明已经部分完成了reduce
  3. $[A \rightarrow \beta \gamma \bullet]$: 该item已经读取完$\beta \gamma$, 并且a作为前瞻符号符合A的语法, 因此完成reduce

以下是括号语法的全部LR(1) items:

[Goal $\rightarrow$ $\bullet$ List, eof]
[Goal $\rightarrow$ List $\bullet$, eof]
[List $\rightarrow$ $\bullet$ List Pair, eof]
[List $\rightarrow$ $\bullet$ List Pair, $\underline{(}$]
[List $\rightarrow$ List $\bullet$ Pair, $\underline{(}$]
[List $\rightarrow$ List $\bullet$ Pair, eof]
[List $\rightarrow$ List Pair $\bullet$, eof]
[List $\rightarrow$ List Pair $\bullet$, $\underline{(}$]
[List $\rightarrow$ $\bullet$ Pair, eof]
[List $\rightarrow$ $\bullet$ Pair, $\underline{(}$]
[List $\rightarrow$ Pair $\bullet$, eof]
[List $\rightarrow$ Pair $\bullet$, $\underline{(}$]
[Pair $\rightarrow$ $\bullet$ $\underline{(}$Pair$\underline{)}$, eof]
[Pair $\rightarrow$ $\bullet$ $\underline{(}$Pair$\underline{)}$, $\underline{)}$]
[Pair $\rightarrow$ $\bullet$ $\underline{(}$Pair$\underline{)}$, $\underline{)}$]
[Pair $\rightarrow$ $\underline{(}$ $\bullet$ Pair$\underline{)}$, eof]
[Pair $\rightarrow$ $\underline{(}$ $\bullet$ Pair$\underline{)}$, $\underline{)}$]
[Pair $\rightarrow$ $\underline{(}$ $\bullet$ Pair$\underline{)}$, $\underline{(}$]
[Pair $\rightarrow$ $\underline{(}$Pair $\bullet$ $\underline{)}$, eof]
[Pair $\rightarrow$ $\underline{(}$Pair $\bullet$ $\underline{)}$, $\underline{)}$]
[Pair $\rightarrow$ $\underline{(}$Pair $\bullet$ $\underline{)}$, $\underline{(}$]
[Pair $\rightarrow$ $\underline{(}$Pair$\underline{)}$ $\bullet$, eof]
[Pair $\rightarrow$ $\underline{(}$Pair$\underline{)}$ $\bullet$, $\underline{)}$]
[Pair $\rightarrow$ $\underline{(}$Pair$\underline{)}$ $\bullet$, $\underline{(}$]
[Pair $\rightarrow$ $\bullet$ $\underline{(}$ $\underline{)}$, eof]
[Pair $\rightarrow$ $\bullet$ $\underline{(}$ $\underline{)}$, $\underline{(}$]
[Pair $\rightarrow$ $\bullet$ $\underline{(}$ $\underline{)}$, $\underline{)}$]
[Pair $\rightarrow$ $\underline{(}$ $\bullet$ $\underline{)}$, eof]
[Pair $\rightarrow$ $\underline{(}$ $\bullet$ $\underline{)}$, $\underline{(}$] 
[Pair $\rightarrow$ $\underline{(}$ $\bullet$ $\underline{)}$, $\underline{)}$]
[Pair $\rightarrow$ $\underline{(}$ $\underline{)}$ $\bullet$, eof]
[Pair $\rightarrow$ $\underline{(}$ $\underline{)}$ $\bullet$, $\underline{(}$] 
[Pair $\rightarrow$ $\underline{(}$ $\underline{)}$ $\bullet$, $\underline{)}$]

需要特别说明其中两个items: 第一个是[Goal $\rightarrow$ $\bullet$ List, eof], 表示parser的初始状态, 此时parser正寻找一个可reduce为Goal的字符串, 每个parser都是从该状态开始; 第二个是[Goal $\rightarrow$ List $\bullet$, eof], 表示parser期望的最终状态, 即parser找到一个可reduce为Goal的字符串. 所以语法分析都是从第一个item开始, 结束于第二个item.
为构建canonical collection of sets of LR(1) items, 也就是$CC$, parser需要一种算法从初始状态开始, 找出所有状态转移. 该算法包含两个基本操作: closure和goto

  1. closure: 将item中隐含的item添加到集合中, 例如, 现在有一个item [Goal $\rightarrow$ $\bullet$ List, eof], 可以看到 $\bullet$ 之后紧跟了一个nonterminal symbol, 因此该item隐含另外两个items: [List $\rightarrow$ $\bullet$ List Pair, eof]和[List $\rightarrow$ $\bullet$ Pair, eof]
  2. goto: 为模拟parser对于某个语法符号x的转移, 需将item集合中的所有$\bullet$后移一位, 也就是移到x之后.

[Goal $\rightarrow$ $\bullet$ List, eof]作为一个item表示parser的起始状态, 该项构成$CC$中的第一个item集合$CC_0$

1.2.1 The closure Procedure

为计算完整的初始状态$CC_0$m 需要通过closure将初始状态item中的所有隐含item加入到$CC_0$中. 以下是closure的算法实现:

closure(s)
  while (s is still changing)
    for each item [$A \rightarrow \beta \bullet C \delta, a$] $\in$ s
      for each production $C \rightarrow \gamma \in P$
        for each b $\in$ FIRST($\delta a$)
          s $\leftarrow$ s $\cup$ {[$C \rightarrow \bullet \ \gamma, b$]}
  return s

closure()中的参数s是一个item集合, 算法会不断遍历集合中的每个item, 若$\bullet$后面紧跟一个nonterminal symbol C, 则将C的所有production加入到集合中, 并将$\bullet$放置在production开始位置, 依次循环, 直到不再添加新的item.
以$[A \rightarrow \beta \bullet C\delta, a]$为例, 该item说明parser已经读取$\beta$, 如果能reduce出C, 且之后紧跟$\delta a$, 则能reduce为A. 因此新添加的item之后必须紧跟$\delta a$. 假设C的production为$C \rightarrow \gamma$, 则closure()会将$\bullet$放在$\gamma$之前, 其前瞻符号为FIRST($\delta a$). 若$\delta$为$\epsilon$, 则前瞻符号为a.
回到括号语法, 其初始状态的item为[Goal $\rightarrow$ $\bullet$ List, eof], 使用closure()后$CC_0$扩展为item集合:

[Goal $\rightarrow$ $\bullet$ List, eof]
[List $\rightarrow$ $\bullet$ List Pair, eof]
[List $\rightarrow$ $\bullet$ List Pair, (]
[List $\rightarrow$ $\bullet$ Pair, eof]
[List $\rightarrow$ $\bullet$ Pair, (]
[Pair $\rightarrow$ $\bullet$ (Pair), eof]
[Pair $\rightarrow$ $\bullet$ (Pair), (]
[Pair $\rightarrow$ $\bullet$ (), eof]
[Pair $\rightarrow$ $\bullet$ (), (]

1.2.2 The goto Procedure

以下是goto的算法实现:

goto(s, x)
  moved $\leftarrow \phi$
  for each item i ∈ s
    if the form of i is [$\alpha \rightarrow \beta \bullet x\delta, a$] then
      moved $\leftarrow$ moved $\cup$ {[$\alpha \rightarrow \beta x \bullet \delta, a$]}
  return closure(moved)

goto()函数有两个参数, s表示item集合, x表示语法符号. goto()会遍历s中的所有item, 若$cdot$后紧跟x, 则将$\bullet$后移一位, 并将新的item加入到集合moved中, 最后调用closure()获得完备集合. 以上一节的$CC_0$为例, goto($CC_0, \underline{(}$)的返回为:

[Pair $\rightarrow$ ( $\bullet$ Pair), eof] 
[Pair $\rightarrow$ ( $\bullet$ Pair), (] 
[Pair $\rightarrow$ ( $\bullet$ ), eof]
[Pair $\rightarrow$ ( $\bullet$ ), (] 
[Pair $\rightarrow$ $\bullet$ (Pair), )] 
[Pair $\rightarrow$ $\bullet$ (), )]

1.2.3 The Canonical Collection for the Parentheses Grammar

有了closure()和goto()后就可以构建canonical collection of sets of LR(1) items. 从$CC_0$开始, 不断后移$cdot$, 直到所有$CC_i$的所有item都递到句尾. 以下是算法实现:

$CC_0$ $\leftarrow$ closure({[S' $\rightarrow \bullet$ S, eof]})
$CC$ $\leftarrow$ {$CC_0$}
while (new sets are still being added to $CC$)
  for each unmarked set $CC_i \in CC$
    mark $CC_i$ as processed
    for each x following a $\bullet$ in an item in $CC_i$
      temp $\leftarrow$ goto($CC_i$, x)
      if temp $\notin CC$
        then $CC \leftarrow CC \ \cup$ {temp}
      record transition from $CC_i$ to temp on x

需要注意的是, $CC$集合只会单调扩张, 并不会缩小. 假设该语法存在n个LR(1) items, 则$CC$中最多存在$2^n$个item set. 以括号语法为例, 其$CC_0$集合如下:

[Goal $\rightarrow \bullet$ List, eof]
[List $\rightarrow \bullet$ List Pair, eof]
[List $\rightarrow \bullet$ List Pair, (]
[List $\rightarrow \bullet$ Pair, eof]
[List $\rightarrow \bullet$ Pair, (]
[Pair $\rightarrow \bullet$ (Pair), eof]
[Pair $\rightarrow \bullet$ (Pair), (]
[Pair $\rightarrow \bullet$ (), eof]
[Pair $\rightarrow \bullet$ (), (]
  1. 第一次迭代: $CC_0$中的$\bullet$紧跟三种语法符号: List, Pair和$\underline{(}$, 所以可以生成三个item集合:
  2. $CC_1$: goto($CC_0$, List) 
    [Goal $\rightarrow$ List $\bullet$, eof] 
    [List $\rightarrow$ List $\bullet$ Pair, eof] 
    [List $\rightarrow$ List $\bullet$ Pair, (]
    [Pair $\rightarrow$ $\bullet$ (Pair), eof] 
    [Pair $\rightarrow$ $\bullet$ (Pair), (] 
    [Pair $\rightarrow$ $\bullet$ (), eof]
    [Pair $\rightarrow$ $\bullet$ (), (]
  3. $CC_2$: goto($CC_0$, Pair) 
    [List $\rightarrow$ Pair $\bullet$, eof]
    [List $\rightarrow$ Pair $\bullet$, (]
  4. $CC_3$: goto($CC_0, \underline{(}$) 
    [Pair $\rightarrow$ $\bullet$ (Pair), )]
    [Pair $\rightarrow$ ( $\bullet$ Pair), eof]
    [Pair $\rightarrow$ ( $\bullet$ Pair), (]
    [Pair $\rightarrow$ $\bullet$ (), )]
    [Pair $\rightarrow$ ( $\bullet$ ), eof]
    [Pair $\rightarrow$ ( $\bullet$ ), (]
  5. 第二次迭代: 从$CC_1$, $CC_3$推导新的item集合, 产生的4个新的item集合:
  6. $CC_4$: goto($CC_1$, Pair) 
    [List $\rightarrow$ List Pair $\bullet$, eof]
    [List $\rightarrow$ List Pair $\bullet$, (]
  7. $CC_5$: goto($CC_3$, Pair) 
    [Pair $\rightarrow$ (Pair$ \bullet$  ), eof]
    [Pair $\rightarrow$ (Pair$ \bullet$ ), (]
  8. $CC_6$: goto($CC_3, \underline{)}$) 
    [Pair $\rightarrow$ $\bullet$ (Pair), )]
    [Pair $\rightarrow$ ( $\bullet$ Pair), )]
    [Pair $\rightarrow$ $\bullet$ (), )]
    [Pair $\rightarrow$ ( $\bullet$ ), )]
  9. $CC_7$: goto($CC_3, \underline{)}$) 
    [Pair $\rightarrow$ () $\bullet$, eof]
    [Pair $\rightarrow$ () $\bullet$, (]
  10. 第三次迭代: 从$CC_5$, $CC_6$推导新的item集合, 产生的3个新的item集合:
  11. $CC_8$: goto($CC_5, \underline{)}$) 
    [Pair $\rightarrow$ (Pair) $\bullet$, eof] [Pair $\rightarrow$ (Pair) $\bullet$, (]
  12. $CC_9$: goto($CC_6, Pair$) 
    [Pair $\rightarrow$ (Pair $\bullet$ ), )]
  13. $CC_{10}$: goto($CC_6, \underline{(}$) 
    [Pair $\rightarrow$ () $\bullet$, )]
  14. 第四次迭代: 从$CC_9$推导新的item集合, 产生1个新的item集合:
  15. $CC_{11}$: goto($CC_9, \underline{)}$) 
    [Pair $\rightarrow$ (Pair) $\bullet$, )]

以下是括号语法canonical collection中的所有item集合的转换图:

item Goal List Pair $\underline{(}$ $\underline{)}$ eof
$CC_0$ $\phi$ $CC_1$ $CC_2$ $CC_3$ $\phi$ $\phi$
$CC_1$ $\phi$ $\phi$ $CC_4$ $CC_3$ $\phi$ $\phi$
$CC_2$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$
$CC_3$ $\phi$ $\phi$ $CC_5$ $CC_6$ $CC_7$ $\phi$
$CC_4$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$
$CC_5$ $\phi$ $\phi$ $\phi$ $\phi$ $CC_8$ $\phi$
$CC_6$ $\phi$ $\phi$ $CC_9$ $CC_6$ $CC_{10}$ $\phi$
$CC_7$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$
$CC_8$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$
$CC_9$ $\phi$ $\phi$ $\phi$ $\phi$ $CC_{11}$ $\phi$
$CC_{10}$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$
$CC_{11}$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$ $\phi$

1.2.4 Filling in the Tables

拥有canonical collection后就可以开始创建Action表和Goto表, 每个$CC_i$都作为一个parser的状态. Action表中会对三种情况产生表项:

  1. $[A \rightarrow \beta \bullet c \gamma, a]$: 表示parser遇到terminal symbol c, 这时只需向前移位. $\beta$和$\gamma$可以为$\epsilon$
  2. $[A \rightarrow \beta \bullet, a]$: 表示parser已识别完毕handle, 可reduce为A
  3. $[S' \rightarrow S \bullet, eof]$: 表示parser识别到目标状态, 表示语法分析成功

Goto只针对一种情况: $[A \rightarrow \beta \bullet C \gamma]$, 其中C为nonterminal symbol, 说明parser需要展开C. 以下是LR(1)的填表算法:

for each $CC_i \in CC$
  for each item $I \in CC_i$
    if I is [$A \rightarrow \beta \bullet c \gamma$,a] and goto($CC_i$,c) = $CC_j$ then
      Action[i, c] $\leftarrow$ "shift j"
    else if I is [$A \rightarrow \beta \ \bullet$, a] then
      Action[i, a] $\leftarrow$ "reduce $A \rightarrow \beta$"
    else if I is [$S' \rightarrow S \ \bullet$, eof] then
      Action[i, eof] $\leftarrow$ "accept"
  for each $n \in NT$
    if goto($CC_i$, n) = $CC_j$ then
      Goto[i, n] $\leftarrow$ j

该算法中忽略了$\bullet$后紧跟nonterminal symbol的情况, 因为parser会使用Goto表不断展开nonterminal symbol直到找到一个terminal symbol, 因此reduce和accpet只针对terminal symbol. 以下是括号算法handle查找的DFA图: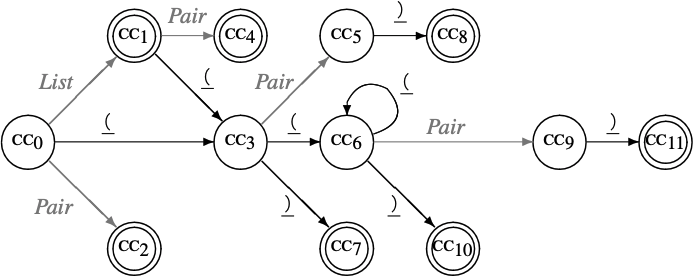
Handle-Finding DFA for the Parentheses

LR(1) parser运行时会交错进行两种操作: shift和reduce. shift表示DFA中两个中间状态之间的转移, 并将沿途的handle和状态压入栈中; reduce表示从中间状态到目标状态的转移, 并将状态和handle从栈中弹出, 让过去的状态浮现在栈顶, parser再利用旧状态, 前瞻符号和Goto表来继续寻找handle. 无论是shift还是reduce, 都存在状态的转移, 唯一区别在于是否将状态和handle加入栈中或从栈中弹出.

1.3 Errors in the Table Construction

以if-then-else结构的二义性语法为例, 其语法如下:

1 $Goal \rightarrow Stmt$
2 $Stmt \rightarrow \text{if expr then} \ Stmt$
3      $| \ \text{if expr then} \ Stmt \ \text{else} \ Stmt$
4      $| \ \text{assign}$

首先根据初始状态[Goal $\rightarrow$ $\bullet$ Stmt, eof]来生成第一个item集合$CC_0$:

[$\textit{Goal}$ $\rightarrow$ $\bullet$ $\textit{Stmt}$, eof] 
[$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$, eof]
[$\textit{Stmt}$ $\rightarrow$ $\bullet$ assign, eof] 
[$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$ else $\textit{Stmt}$, eof]
  1. 第一次迭代: 根据$CC_0$中的$\bullet$紧跟的语法符号进行转移, 生成三个新的item集合:
  2. $CC_1$: goto($CC_0$, Stmt) 
    [$\textit{Goal}$ $\rightarrow$ $\textit{Stmt}$ $\bullet$,eof]
  3. $CC_2$: goto($CC_0$, if) 
    [$\textit{Stmt}$ $\rightarrow$ if $\bullet$ expr then $\textit{Stmt}$ ,eof],
    [$\textit{Stmt}$ $\rightarrow$ if $\bullet$ expr then $\textit{Stmt}$ else $\textit{Stmt}$ ,eof]
  4. $CC_3$: goto($CC_0$, assign) 
    [$\textit{Stmt}$ $\rightarrow$ assign $\bullet$, eof]
  5. 第二次迭代: 由于$CC_1$和$CC_3$已经完成转移, 只需从$CC_2$出发, 对expr符号进行转移, 得到一个新的item集合:
  6. $CC_4$: goto($CC_2$, expr) 
    [$\textit{Stmt}$ $\rightarrow$ if expr $\bullet$ then $\textit{Stmt}$, eof],
    [$\textit{Stmt}$ $\rightarrow$ if expr $\bullet$ then $\textit{Stmt}$ else Stmt}$, eof]
  7. 第三次迭代: 从$CC_4$出发, 对then符号进行转移, 得到一个新的item集合:
  8. $CC_5$: goto($CC_4$, then) 
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\bullet$ $\textit{Stmt}$, eof],
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\bullet$ $\textit{Stmt}$ else $\textit{Stmt}$, eof],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ assign, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$ else $\textit{Stmt}$, {eof, else}]
  9. 第四次迭代: 从$CC_5$出发, 对Stmt, if和assign进行转移, 得到三个新的item集合
  10. $CC_6$: goto($CC_5$, Stmt) 
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ $\bullet$, eof],
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ $\bullet$ else $\textit{Stmt}$, eof]
  11. $CC_7$: goto($CC_5$, if) 
    [$\textit{Stmt}$ $\rightarrow$ if $\bullet$ expr then $\textit{Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ if $\bullet$ expr then $\textit{Stmt}$ else $\textit{Stmt}$, {eof, else}]
  12. $CC_8$: goto($CC_5$, assign) 
    [$\textit{Stmt}$ $\rightarrow$ assign $\bullet$, {eof, else}]
  13. 第五次迭代: 对$CC_6$的else符号和$CC_7$的expr符号进行转移, 生成2个新的item集合:
  14. $CC_9$: goto($CC_6$, else) 
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ else $\bullet$ $\textit{Stmt}$, eof],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$, eof],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$ else $\textit{Stmt}$, eof],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ assign, eof]
  15. $CC_{10}$: goto($CC_7$, expr) 
    [$\textit{Stmt}$ $\rightarrow$ if expr $\bullet$ then $\textit{Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ if expr $\bullet$ then $\textit{Stmt}$ else $\textit{Stmt}$, {eof, else}]
  16. 第六次迭代: 对$CC_9$的Stmt符号和$CC_{10}$的then符号进行转移, 生成2个新的item集合:
  17. $CC_{11}$: goto($CC_9$, Stmt) 
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ else $\textit{Stmt}$ $\bullet$, eof]
  18. $CC_{12}$: goto($CC_{10}$, then) 
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\bullet$ $\textit{Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\bullet$ $\textit{Stmt}$ else Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$ else Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ assign, {eof, else}]
  19. 第七次迭代: 对$CC_{12}$的Stmt符号进行转移, 获得1个新的item集合:
  20. $CC_{13}$: goto($CC_{12}$, Stmt) 
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ $\bullet$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ $\bullet$ else $\textit{Stmt}$, {eof, else}]
  21. 第八次迭代: 对$CC_{13}$的else符号进行转移, 获得1个新的item集合:
  22. $CC_{14}$: goto($CC_{13}$, else) 
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ else $\bullet$ Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ if expr then $\textit{Stmt}$ else $\textit{Stmt}$, {eof, else}],
    [$\textit{Stmt}$ $\rightarrow$ $\bullet$ assign, {eof, else}]
  23. 第九次迭代: 对$CC_15$的Stmt符号进行转移, 获得1个新的item集合:
  24. $CC_{15}$: goto($CC_{14}$, Stmt) 
    [$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ else $\textit{Stmt}$ $\bullet$, {eof, else}]

其中, $CC_{13}$中的item存在shift-reduce conflict: 

[$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ $\bullet$, eof],
[$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ $\bullet$ else $\textit{Stmt}$, eof]
[$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ $\bullet$, else],
[$\textit{Stmt}$ $\rightarrow$ if expr then $\textit{Stmt}$ $\bullet$ else $\textit{Stmt}$, else]

但parser解析到else或eof时, 可选择reduce为Stmt, 也可选择shift到其他状态, 这种冲突是语法的二义性导致的问题. 除了shift-reduce conflict, 还存在reduce-reduce conflict, 例如: $[A \rightarrow \gamma \delta \bullet, a]$和$[B \rightarrow \gamma \delta \bullet, a]$, 前瞻符号a会导致A和B的reduce冲突, 需要重构语法来消除二义性.

2. Practical Issues

2.1 Error Recovery

当编译包含语法错误的代码时, 编译器会汇报尽量多的语法错误. 但上述所讲述的parser遇到语法错误就会停止运行, 这导致每次编译只能汇报一个语法错误. 为了在一次编译中找到尽量多的语法错误, 需要一种从错误中恢复的机制: 转换到另一个状态. 当parser遇到一个语法错误时, 会不断丢弃输入字符, 直到找到一个synchronizing word(同步单词), 并将内部状态重置为与同步按此相一致的状态. 很多语法以semicolon(分号)作为单个语句的终止符, 因此parser检测到错误时可直接抛弃整条语句, 直到找到下一个semicolon, 并将状态重置为成功识别语句的目标状态.
对于LR(1) parser, 再同步机制更为负责. Parser需要不断丢弃输入, 直到找到semicolon; 接下从上到下扫描栈, 直到找到一个非错误表项.

2.2 Unary Operators

表达式语法只包含二元运算符, 但代数运算包含大量一元运算符, 如负号. 程序设计语言中也存在很多一元运算符, 如递增, 递减, 取址, 引用, 取反. 向表达式语法添加一元运算符时应谨慎处理.
一般来说, 一元运算符的优先级高于二元运算符, 例如一元绝对值运算符$||$, 其优先级高于$\times$和$\div$, 但低于Factor, 以便使用$||$对括号内的表达式求值. 以下是添加了绝对值后的语法:

0  $\textit{Goal} \rightarrow \textit{Expr}$
1  $\textit{Expr} \rightarrow \textit{Expr} + \textit{Term}$
2      | $\textit{Expr} - \textit{Term}$
3      | $\textit{Term}$
4  $\textit{Term} \rightarrow \textit{Term} \times \textit{Value}$
5      | $\textit{Term} \div \textit{Value}$
6      | $\textit{Value}$
7  $\textit{Value} \rightarrow || \ \textit{Factor}$
8      | $\textit{Factor}$
9  $\textit{Factor} \rightarrow ( \ \textit{Expr} \ )$
10     | num
11     | name

2.3 Handle Context-Sensitive Ambiguity

当使用一个单词或符号来表示两种不同语义时, 可能导致语法二义性. 以早期程序设计语言为例, 它们会用括号来表示函数参数和数组下标, 其语法如下:

1 $\textit{Factor} \rightarrow \textit{FunctionReference}$
2      | $\textit{ArrayReference}$
3      | ( $\textit{Expr}$ )
4      | num
5      | name
6 $\textit{FunctionReference} \rightarrow$ name ( $\textit{ArgList}$ )
7 $\textit{ArrayReference} \rightarrow$ name ( $\textit{ArgList}$ )

面对代码为$fee(i, j)$时, parser不知道fee是二维数组还是函数名称, 因为FunctionReference和ArrayReference产生了reduce-reduce conflict. 这时有两种方法解决, 一个是重写语法, 将函数参数和数组引用合并为一个产生式, 将问题拖延到后续步骤解决; 或通过声明类型归类标识符, 修改为以下语法:

$\textit{FunctionReference} \rightarrow$ function-name ( $\textit{ArgList}$ )
$\textit{ArrayReference} \rightarrow$ variable-name ( $\textit{ArgList}$ )

2.4 Left Versus Right Recursion

Top-down parser需要使用右递归语法, 而buttom-up parser可适应左递归或右递归语法, 因此需要在左右递归之间做出一个选择. 通常需要考虑以下两个因素:

2.4.1 Stack Depth

一般来说, 左递归使用的栈深度较小, 以下列语法为例:

  1. 左递归语法: 先将$elt_1$压入栈中, 将其reduce为List; 然后将$elt_2$压入栈中, reduce为List, 以此类推, 将剩下的所有elt压入并reduce为List. 栈的最大深度为2.
    $\textit{List} \rightarrow \textit{List} \ \text{elt}$
        | $\text{elt}$
  2. 右递归语法: 将所有elt压入栈中, 取出$elt_5$并reduce为List, 并以此类推, 将栈中剩下的elt弹出并reduce为List. 栈的最大深度为5.
    $\textit{List} \rightarrow \text{elt} \ \textit{List}$
        | $\text{elt}$

右递归语法需要更多栈空间, 其最大栈深度与输入字符的数量相关; 左递归语法的最大深度则取决于语法本身, 与输入流无关.

2.4.2 Associativity

左递归语法具有左结合性, 右递归语法具有右结合性. 对于输入$X_1 + X_2 + X_3$来说, 左递归语法遵守从左到右的求值顺序, 等同于$(X_1 + X_2) + X_3$; 右递归语法遵守从右到左的求值顺序, 等同于$X_1 + (X_2 + X_3)$, 两种语法都可获得正确结果. 但对于$X_1 - X_2 + X_3$, 左递归等同于$(X_1 - X_2) + X_3$, 右递归等同于$X_1 - (X_2 + X_3)$, 两者会造成全完不同的结果. 因此必须遵守语言规定的求值次序, 并谨慎的生成intermediate
representation, 以反映正确的结合性.

3. Advanced Topics

3.1 Optimize a Grammar

语法本身对解析语法的工作量有直接影响. Top-down parser和button-up parser都需要构建推导: Top-down parser对每个production进行expand(扩展); Button-up parser对每个production进行reduce(规约). 若production较短, 则语法分析的所需时间就会较短.
通常可通过重写语法来降低parser tree的高度, 以此减少expand或reduce的操作次数. 以括号语法为例, 输入流$a + 2 x b$的parse tree如下: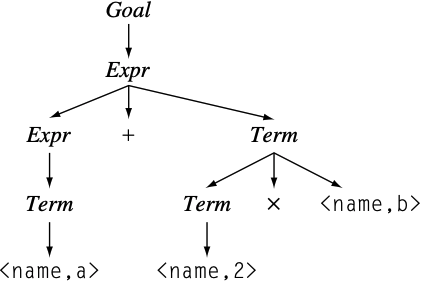
Parse Tree for a + 2 x b (1)

任何只有一个子节点的内部节点都是优化的候选者, 可将Factor添加到Term中, 如下:

1 $\textit{Term} \rightarrow \textit{Term} \ \times \ ( \ \textit{Expr} \ )$
2     | $\textit{Term}$ $\times$ name
3     | $\textit{Term}$ $\times$ num
4     | $\textit{Term}$ $\div$ $( \ \textit{Expr} \ )$
5     | $\textit{Term}$ $\div$ name
6     | $\textit{Term}$ $\div$ num
7     | ( $\textit{Expr}$ )
8     | name
9     | num

以下是parse tree: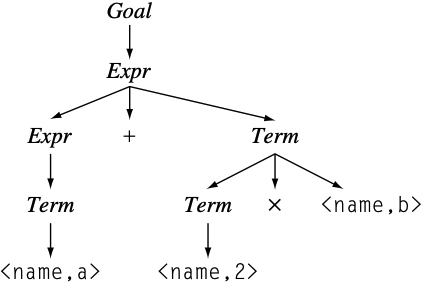
Parse Tree for a + 2 x b (2)

语法优化后, 消除了3个reduce操作, 但shift操作数量不变. 一般来说, production只含有一个符号都是可以折叠起来, 这种production被称为useless production; 但有时这种production可是的语法更为紧凑, 更具有可读性.

3.2 Reduce the Size of LR(1) Table

本节将介绍三种缩小LR(1) table的方法, 以下是代数表达式的Action table和Goto table:
Action Table for the Classic Expression Grammar
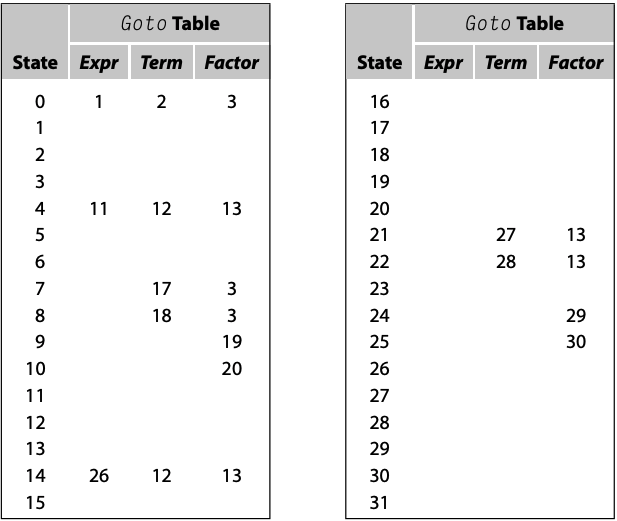
Goto Table for the Classic Expression Grammar

  1. Combine Rows or Columns
    若存在两行或者两列拥有相同表项, 则可以合并两者. Action table中第7行到第10行相同, 第4, 14, 21, 22, 24和25行也相同, 因此只需要实现一次. 合并后Action表减少9行, 节省了28%空间. 合并行列虽然能直接减小表体积, 但可能降低表的访问速度, 因为需要添加一个额外的表访问方式, 必须在内存访问和内存空间之间做出权衡.

  2. Shrink the Grammar
    通过重写语法来减少production数量来缩小表体积. 例如: 将$\times$和$\div$合并为terminal symbol muldiv, 将$+$和$-$合并为terminal symbol addsub, 将num和name合并为一个符号val. 重写后的语法如下:

    1 $\textit{Goal} \rightarrow \textit{Expr}$
    2 $\textit{Expr} \rightarrow \textit{Expr}$ addsub $\textit{Term}$
    3     | $\textit{Term}$
    4 $\textit{Term} \rightarrow \textit{Term}$ muldiv $\textit{Factor}$
    5     | $\textit{Factor}$
    6 $\textit{Factor}$ $\rightarrow$ $( \ \textit{Expr} \ )$
    7     | val

    Action table因此减少了三列.

  3. Directly Encoding the Table
    作为最终的改进方式, parser generator可直接放弃table-driven skeleton parser, 而选择hard-coded方式, 将每个状态变成一个小的case语句来替代Action table和Goto table. 这种方式可避免表示Action table和Goto table中的空表项, 也就是语法错误的表项. 使用适当的代码布局技术, 生成的parser在instruction cache和paging system中呈现出很强的局部性; 缺点在于, 这种方式生成的代码几乎不可读.

  4. Use Other Construction Algorithms
    除了canonical LR(1), 还有一些其他的LL parser. 例如: SLR(1), LALR(1)就和lookahead LR(1), 这些算法都可以生成更小的表. 但这些算法也存在一些局限性, canonical LR(1)相比之下还是最通用的构造法. 虽然产生的表体积最大, 但可接受的语法范畴也最大.